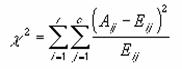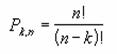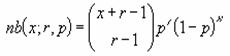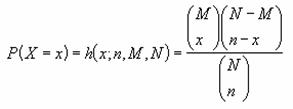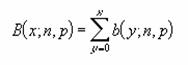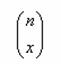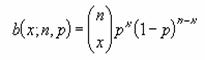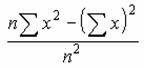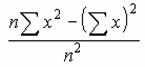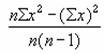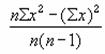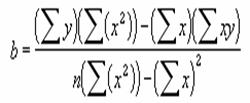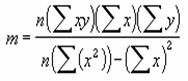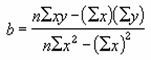
�������Ǝw���Ȑ�
�����ŏЉ����́A�����I���邢�͎w���Ȑ��I�ɕϓ����鉿�i�Ȃǂ̏������l��\�����邽�߂ɗ��p���܂��B�z���œ��͂���ƕ����̌��ʂ��P�̐����ŋ��߂邱�Ƃ��ł��܂��B
TREND �����I�ȕϓ��l��Ԃ��܂��B
LINEST �����I�ȕϓ��W���̒l��Ԃ��܂��B
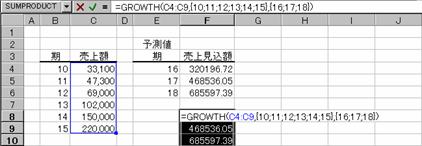
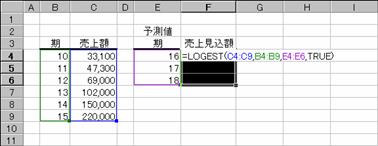
GROWTH �w���Ȑ��I�ȕϓ��l��Ԃ��܂��B
LOGEST �w���Ȑ��I�ȕϓ��W���̒l��Ԃ��܂��B
INTERCEPT ��A�����̐ؕЂ̒l��Ԃ��B
���s�q�d�m�c��
���m��y�Ɗ��m��x�̃f�[�^���ɓ��Ă͂�(�ŏ����@���g����)�A���̒�����ŁA�w�肵���V����x�̔z��ɑ���y�̒l���ߎ��I�Ɍv�Z���܂��B
���� TREND(���m��y, ���m��x, �V����x, �萔)
���m��y ���ɂ킩���Ă���y�̒l�̌n��iy=mx+b�j
�� ���m��y�̔z��1�̗�ɓ��͂���Ă���ꍇ�A���m��x�̊e��͂��ꂼ��قȂ�ϐ��ł���ƌ��Ȃ����
���m��x ���ɂ킩���Ă���x�̒l�̌n��iy=mx+b�j
�� ���m��x�̔z��ɂ́A1�܂��͕����̕ϐ��̌n����w�肷�邱�Ƃ��ł���B�ϐ��̌n�� 1 �ł���ꍇ�A���m��y �� ���m��x �́A���҂̎����������ł���A�ǂ̂悤�Ȍ`�͈̔͂ł����Ă����܂��܂���B�ϐ��̌n�����ł���ꍇ�A���m��y��1�s�܂���1��͈̔͂łȂ���Ȃ�܂���B
�� ���̈����͏ȗ��B�ȗ�����ƁA���m��y�Ɠ����T�C�Y�z��ł���ƌ��Ȃ����
�V����x �Ή�����x�̒l���w�肷��
�� �V����x�ɂ́A���m��x �Ɠ��l�A���ꂼ��Ɨ������ϐ������͂���Ă��� 1 �̗� (�܂��� 1 �̍s) ���w�肷��K�v������܂��B���̌��ʁA���m��y �� 1 �̗�ɓ��͂���Ă���ꍇ�A���m��x �� �V����x �͓����łȂ���Ȃ�܂���B�܂��A���m��y �� 1 �̍s�ɓ��͂���Ă���ꍇ�A���m��x �� �V����x �͓����s���łȂ���Ȃ�܂���B
�� ���̈������ȗ�����ƁA���m��x�Ɠ����l�ł���ƌ��Ȃ���܂��B
�� ���m��x�ƐV����x�̗������ȗ�����ƁA���m��y�Ɠ����T�C�Y�̔z��ł���ƌ��Ȃ����B
�萔 �萔b��0�ɂ��邩�ǂ������A�_���l�Ŏw�肵�܂��B
�� �萔 �� TRUE ���w�肷�邩�ȗ�����ƁAb �̒l���v�Z����܂��B
�� �萔 �� FALSE ���w�肷��ƁAb �̒l�� 0(�[��) �ɐݒ肳��Ay =
mx �ƂȂ�悤�� m �̒l����������܂��B
�����m���m��x�n���ȗ�����ƈ����m���m��y�n�Ŏw�肵�����X�g�Ɠ������̂P����n�܂�A�Ԕz��{1;2;3;4;5;6;7;�E�E�E}������l�Ƃ��č̗p����܂��B
�g�p��
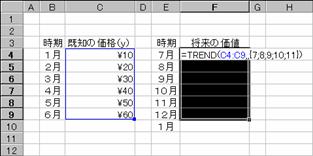
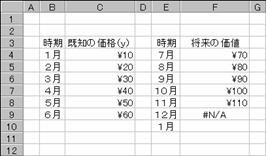
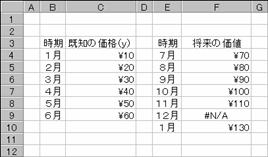
���鉿�l�������ȐL�т������Ă���Ƃ��̉��i�̐L�т�\�����Ă݂܂��傤�B�}�`�͋��߂���l���ǂ̂悤�ɕω����邩���m�F���邽�߂ɁA���Ԋu�ő����ނ���f�[�^�̏������l�����߂Ă��܂��B
�@���ʂ�\������Z���͈͂�I������
�A��������͂���
���m�r�g�h�e�s�n�{�m�b�s�q�k�n�L�[�������Ȃ���m�d���������n�L�[������
�m�`�n���ʂ����߂���
�Z���e�X�̂P�Q���������m�^�`�ɂȂ��Ă���̂́A�I�������͈͂̃Z���������������̐V�������̃f�[�^�������Ȃ����߂ł��B�o�V�G�W�G�X�G�P�O�G�P�P�G�p�Ȃ̂ɑI�������Z���͈͂͂P�Q�����܂ł�����ł��B
 �@EX4A557Z
�@EX4A557Z
 �@EX4A558Z
�@EX4A558Z
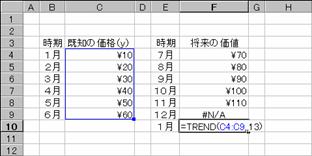
���ʂ��P�������߂�ꍇ�́A�z���ł͂Ȃ��ʏ�̐����Ƃ��ē��͂��܂��B
�@��������͂���
���m�d���������n�L�[������
�m�`�n���ʂ����߂���
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�}�`
 �@
�@
EX4A559Z�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A169Z
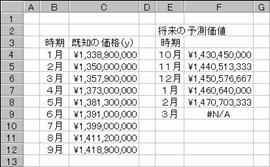
���Z���e�S�`�e�X��I������
����������͂���
���s�q�d�m�c�i�b�S�F�b�P�Q�C�C�o�P�O�G�P�P�G�P�Q�G�P�R�G�P�S�p�j
���m�r�g�h�e�s�n�{�m�b�s�q�k�n�L�[�������Ȃ���m�d���������n�L�[������
�m�`�n���ʂ����߂���
�V����x�͋��߂鏇�Ԃ�\���̂ŁA�}�a�̂悤�ɂP�Q���̎����P���ł����Ă��A�����Ƃ��Ă͂P�R�ɂȂ�܂��B�������ȉ��̂悤�ɂ���Ɛ��������߂��܂���B
���s�q�d�m�c�i�b�S�F�b�P�Q�C�C�o�P�O�G�P�P�G�P�Q�G�P�G�Q�p�j
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@���@��
�}�a
 �@EX4A168Z
�@EX4A168Z
���k�h�m�d�r�s��
�ŏ����@���g���āA�w�肵���f�[�^�ɍł��悭���Ă͂܂钼�����Z�o���A���̒������L�q����W���� y �ؕЂƂ̔z���Ԃ��܂��B���̊��ł́A�l�͔z��Ƃ��ĕԂ���A�z���Ƃ��ē��͂���܂��B
���� LINEST(���m��y, ���m��x, �萔, �)
���m��y ���ɂ킩���Ă���y�̒l�̌n��iy=mx+b�j
���m��x ���ɂ킩���Ă���x�̒l�̌n��iy=mx+b�j
�萔 �萔b�̏������@��_���l�Ŏw�肷��
TRUE �@b�̒l���v�Z����i�ȗ��l�j
FALSE �@b�̒l��0�ɂ���y=mx�ɒ�������
� ��A�����̕���̏��
TRUE ��A�����̕�����Ԃ����
FALSE �W��m�ƒ萔b�݂̂̔z�Ԃ����i�ȗ��l�j
���m��x ���ȗ�����ƁA���m��y �Ɠ����T�C�Y�� {1,2,3,...} �Ƃ����z��ł���ƌ��Ȃ���܂��B���̐������g���� m �� b �̒l���v�Z����܂��B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@
EX4A087Z
EX4A088Z
�g�p��
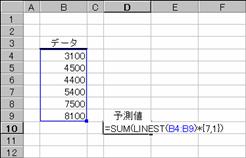
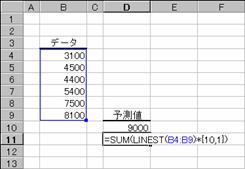
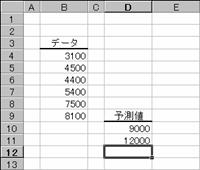
�}�̂悤�ȂU�̃f�[�^������Ƃ��A�V�ڂ̃f�[�^�l��\�����Ă݂܂��傤�B
�@��������͂���
�m�`�n���ʂ����߂���
 �@�@
�@�@
EX4A561Z�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A562Z
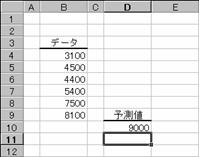
�����悤�ɂP�O�ڂ̃f�[�^�͎��̂悤�ɗ\���ł��܂��B���̊��ł́A�W����Ԃ��̂łr�t�l���Ƃ����Z��g�ݍ��킹�Ēl�����߂�悤�ɂ��܂��B
 �@�@
�@�@
EX4A563Z�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A564Z
���f�q�n�v�s�g��
�w�肳�ꂽ���m��y�Ɗ��m��x�̃f�[�^���g�p���ĐV����x�̔z��ɑ���y�̒l���v�Z���܂��B
���� GROWTH(���m��y, ���m��x, �V����x, �萔)
���m��y ���ɂ킩���Ă���y�̒l�̌n��iy=b*m^x�j
���m��x ���ɂ킩���Ă���x�̒l�̌n��iy=b*m^x�j
�V����x �V����x�̒l���w�肵�܂��B
�萔 �萔b��1�ɂ��邩�ǂ������A�_���l�Ŏw�肵�܂��B
TRUE ���̒l���v�Z����i�ȗ����j
FALSE b�̒l��1�ɐݒ肷��iy=m^x�j
���m��x ���ȗ�����ƁA���m��y �Ɠ����T�C�Y�� �o1,2,3...�p �Ƃ����z����w�肵���ƌ��Ȃ���܂��B
�g�p��
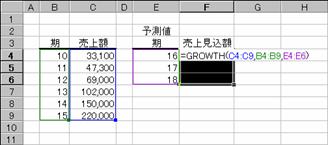
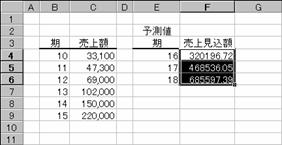
�e���̔���z���珫���̔���z��\������ƁA�}�̂悤�ɋ��߂��܂��B
�@���ʂ�\������Z���͈͂�I������
�A��������͂���
���m�r�g�h�e�s�n�{�m�b�s�q�k�n�L�[�������Ȃ���m�d���������n�L�[������
�m�`�n���ʂ����߂���
���m��x�ƐV����x�𐔎��ɒ��ړ��͂���ꍇ�́A�m�a�n�̂悤�Ɂo�p�ň͂�Œl����͂��܂��B
 �@EX4A552Z
�@EX4A552Z
 �@EX4A553Z
�@EX4A553Z
 �@EX4A554Z
�@EX4A554Z
���k�n�f�d�r�s��
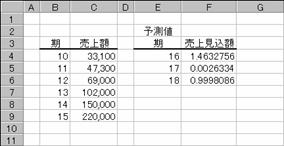
�Ȑ���\���W���̔z��̒l��Ԃ��܂��B
���� LOGEST(���m��y, ���m��x, �萔, �)
���m��y ���ɂ킩���Ă���y�̒l�̌n��iy=b*m^x�j
���m��x ���ɂ킩���Ă���x�̒l�̌n��iy=b*m^x�j
�萔 �萔b��1�ɂ��邩�ǂ������A�_���l�Ŏw�肵�܂��B
TRUE ���̒l���v�Z����i�ȗ����j
FALSE b�̒l��1�ɐݒ肷��iy=m^x�j
� ��A�����̕���̏��
TRUE ��A�����̕�����Ԃ����
FALSE �W��m�ƒ萔b�݂̂̔z�Ԃ����i�ȗ��l�j
�w���Ȑ��͎��̐����ŕ\����܂��B
y = b*m^x
�܂��A�Ɨ��ϐ�����������ꍇ��
y =
(b*(m1^x1)*(m2^x2)*_)
�g�p��
�f�q�n�v�s�g���Ɠ����f�[�^���g���Č��ʁi�W���j�����߂Ă݂܂��傤�B
�@���ʂ�\������Z���͈͂�I������
�A��������͂���
���m�r�g�h�e�s�n�{�m�b�s�q�k�n�L�[�������Ȃ���m�d���������n�L�[������
�m�`�n���ʂ����߂���
 �@EX4A555Z
�@EX4A555Z
 �@EX4A556Z
�@EX4A556Z
���h�m�s�d�q�b�d�o�s��
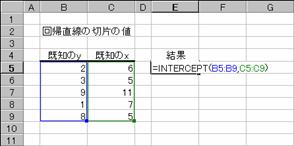
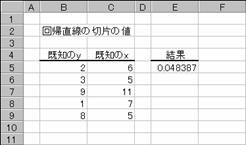
���m��x�Ɗ��m��y��ʉ߂�����`��A�����̐ؕЁi���m��x�Ɗ��m��y�̒l��ʉ߂����A������y���ƌ������W�j���v�Z���܂��B���̐ؕЂ́A
���� INTERCEPT(���m��y, ���m��x)
���m��y �ϑ��܂��̓f�[�^�̏]���͈͂��w�肷��
���m��x �ϑ��܂��̓f�[�^�̓Ɨ��͈͂��w�肷��
��A�����̐ؕЂ́A���̐����ŕ\����܂��B
�@�@�@�@�@�@�@�@�@�@�@�@EX4A083Z
�܂��A��A�����̌X���́A���̐����ŕ\����܂��B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A084Z
�g�p��
�m�`�n��������͂���
�m�a�n����
 |
|||
 |
|||
 �@
�@
EX4A393Z�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A394Z
�y�܂Ƃ߁z
TREND ������̒l��Ԃ��܂��B
LINEST �����̌W���̒l��Ԃ��܂��B
GROWTH �w���Ȑ���̒l��Ԃ��܂��B
LOGEST �w���Ȑ��̌W���̒l��Ԃ��܂��B
INTERCEPT ��A�����̐ؕЂ̒l��Ԃ��B
����W�c�ƕW�{�̕��U
����l�̏W�܂�ɑ��镪�U�����߂���͎��̂S������܂��B�l�̏W�܂���W�c�̕W�{�ƌ��Ȃ��Čv�Z������ƕ�W�c�S�̂ƌ��Ȃ��Čv�Z�����������܂��B
VAR�� ��W�c�̕W�{�ɑ��镪�U
VARA�� ��W�c�̕W�{�ɑ��镪�U�i������A�_���l���܂ށj
VARP�� ��W�c�S�̂ƌ��Ȃ������U
VARPA�� ��W�c�S�̂ƌ��Ȃ������U�i������A�_���l���܂ށj
���u�`�q��
�������W�c�̕W�{�ł���ƌ��Ȃ��āA��W�c�ɑ��镪�U��Ԃ��܂��B
���� VAR(���l1, ���l2, ...)
���l1, ���l2, ... ��W�c�̕W�{�ɑΉ����鐔�l���w�肷��i�ő�R�O�j
���l�ɕ�����A�_���l�A�Z���͖�������܂��B���̊��͎��̐������g���ĕ��U���v�Z����܂��B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A109Z
���u�`�q�`��
�W�{�ɑ��镪�U���v�Z���܂��B�������ATRUE�AFALSE�Ȃǂ̘_���l���v�Z�̑ΏۂƂȂ�B
���� VARA(���l1, ���l2,...)
���l1, ���l2, ... ��W�c�̕W�{�ɑΉ����鐔�l���w�肷��i�ő�R�O�j
������TRUE���܂܂�Ă���ꍇ��1�ƌ��Ȃ���A������܂���FALSE���܂܂�Ă���ꍇ��0
(�[��)�ƌ��Ȃ���܂��B���̊��͎��̐������g���ĕ��U���v�Z����܂��B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A110Z
���u�`�q�o��
�������W�c�S�̂ł���Ɖ��肵�āA��W�c�̕��U��Ԃ��܂��B
���� VARP(���l1, ���l2, ...)
���l1, ���l2, ... ��W�c�S�̂ɑΉ����鐔�l���w�肷��i�ő�R�O�j
���l�Ƃ��ĕ�����A�_���l�A�Z���͖�������܂��B���̊��͎��̐������g���ĕ��U���v�Z����܂��B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A111Z
���u�`�q�o�`��
�������W�c�S�̂ƌ��Ȃ��āA���U���v�Z���܂��B���l�ȊO�ɁA�������ATRUE�AFALSE �Ȃǂ̘_���l���v�Z�̑ΏۂɂȂ�
���� VARPA(���l1, ���l2,...)
���l1, ���l2,... ��W�c�S�̂ɑΉ����鐔�l���w�肵�܂��i�ő�R�O�j
�������W�c�S�̂ł���ƌ��Ȃ��܂��B�w�肷�鐔�l����W�c�̕W�{�ł���ꍇ�́AVARA�����g���ĕ��U���v�Z���܂��B������TRUE���܂܂��ꍇ��1�ƌ��Ȃ���A������܂���FALSE���܂܂��ꍇ��0(�[��)�ƌ��Ȃ���܂��BVARPA
���͎��̐������g���ĕ��U���v�Z���܂��B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A112Z
�g�p��
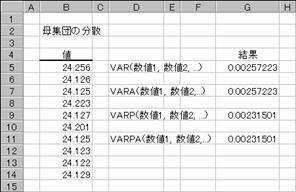
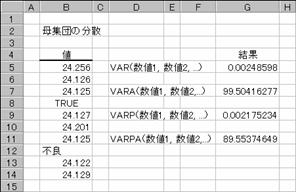
�y��̐��Y���C���Ő������ꂽ���R�[�_�[����10�{��ׂɒ��o���A���Ԃ̓��a�𑪒肵���Ƃ���A�}�`�̒l�ɂȂ�܂����B�����̒l���W�c�̕W�{�ƌ��Ȃ����ꍇ�ƁA��W�c�S�̂ł���Ɖ��肵���ꍇ�̕��U�l���ׂĂ݂܂��傤�B���U�l���傫���Ȃ�A���^�̘V���▀�Ղ��l������̂Ō������������f�ł��܂��B
�}�`�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�}�a
 �@
�@
EX4A191Z�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A192Z
�f�T�@�F���u�`�q�i�a�T�F�a�P�S�j
�f�T�@�F���u�`�q�`�i�a�T�F�a�P�S�j
�f�T�@�F���u�`�q�o�i�a�T�F�a�P�S�j
�f�T�@�F���u�`�q�o�`�i�a�T�F�a�P�S�j
�}�a�ł͕s�Ǖi���s�q�t�d���邢�́h�s�ǁh�ŕ\���āA�s�q�t�d�ƕ����f�[�^���Ȃ����v�Z�l�i�f�T�Ƃf�X�̌��ʁj�Ɗ܂߂��v�Z�l�i�f�V�Ƃf�P�P�̌��ʁj�̈Ⴂ���ׂĂ��܂��B
�y�܂Ƃ߁z
VAR ��W�c�̕W�{���g���ĕ��U��Ԃ��܂��B
VARA ���l�A������A����ј_���l���܂ޕ�W�c�̕W�{���g���ĕ��U��Ԃ��܂��B
VARP ��W�c�S�̂�Ώۂɕ��U��Ԃ��܂��B
VARPA ���l�A������A����ј_���l���܂ޕ�W�c�S�̂�Ώۂɕ��U��Ԃ��܂��B
�����C�u�����z
���v�d�h�a�t�k�k��
���C�u�����z�̒l��Ԃ��B�@�B���̏Ⴗ��܂ł̕��ώ��Ԃ̂悤�ȐM�����̕��͂Ɏg�p����܂��B
���� WEIBULL(x, ��, ��, ���`��)
x ���ɑ�����鐔�l���w�肷��B
�� ���z�̃p�����[�^���w�肷��B
�� ���z�̃p�����[�^���w�肷��B
���`�� �g�p������̌`����_���l�Ŏw�肷��B
�_���l�@�@�v�Z���@
TRUE �ݐϕ��z���Ōv�Z����
FALSE �m�����x���Ōv�Z����
����x<0�̏ꍇ�A��<=0�܂��̓�<=0�ł���ꍇ�A�G���[�l
#NUM! ���Ԃ���܂��B���C�u���ݐϕ��z���͎��P�A���C�u���m�����x���͎��Q�Œ�`����܂��B
�@�@�@���P�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@���Q
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A113Z�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A114Z
��=1�̏ꍇ�A���̎��Œ�`�����w�����z���̒l���v�Z����܂��B
�@�@�@�@�@�@�@�@�@�@�@�@ EX4A115Z
�g�p��
�}�`�ł́A�������������`����ς��Čv�Z���Ă��܂��B
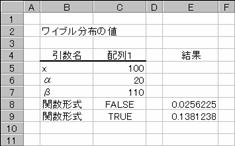 �@EX4A189Z
�@EX4A189Z
�d�W�@�F���v�d�h�a�t�k�k�i���b���T�C���b���U�C���b���V�C�b�W�j
�d�X�@�F���v�d�h�a�t�k�k�i���b���T�C���b���U�C���b���V�C�b�X�j
���ݐϊm�����x��
�ݐϊm�����x���ɂ́A�ݐσ��m�����x���Ƌt��������܂��B�ݐϊm�����x�́A�f�[�^�̊������Z�o����Ƃ��Ɏg�p���܂��B
���a�d�s�`�c�h�r�s��
�ݐσ��m�����x��Ԃ��܂��B�����̕W�{��ΏۂɊ����̕ω��͂���ꍇ�ȂǂɎg�p���܂��B
���� BETADIST(x, ��, ��, A, B)
x ���A�`B�͈̔͂ŁA�]������u�Ԃ��w�肵�܂��B
�� �m�����z�ɑ���p�����[�^���w�肵�܂��B
�� �m�����z�ɑ���p�����[�^���w�肵�܂��B
A x�̋�Ԃ̉������w�肵�܂��i�ȗ��j
B x�̋�Ԃ̏�����w�肵�܂��i�ȗ��j
��<=0�܂��̓�<=0�ł���ꍇ�A���邢��x < A�Ax > B�A�܂��� A = B
�ł���ꍇ�A�G���[�l #NUM! ���Ԃ���܂��B����A�����B���ȗ������ꍇ�A�W���ݐσ����z���g�p����AA = 0 ����� B = 1 �Ƃ��Čv�Z���s���܂��B
�g�p��
�}�`�̃f�[�^�Ŋm�������߂�Ɩ�O�D�T�U�T�X�ł��邱�Ƃ�������܂��B
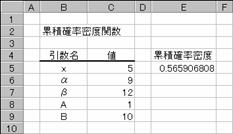 �@EX4A178Z
�@EX4A178Z
�d�T�@�F��BETADIST(C5,C6,C7,C8,C9)
���a�d�s�`�h�m�u��
�ݐσ��m�����x���̋t����Ԃ��܂��B�m��=BETADIST(x,...)�ł���Ƃ��ABETAINV(�m��,...)=x�Ƃ����W�����藧���܂��B
���� BETAINV(�m��, ��, ��, A, B)
�m�� ���m�����z�ɔ����m�����w�肵�܂��B
�� �m�����z�̃p�����[�^���w�肵�܂��B
�� �m�����z�̃p�����[�^���w�肵�܂��B
A x �̋�Ԃ̉������w�肵�܂��i�ȗ��j
B x �̋�Ԃ̏�����w�肵�܂��i�ȗ��j
��<=0 �܂��� ��<=0 �ł���ꍇ�A���邢�͊m��<=0 �܂��� �m�� > 1 �ł���ꍇ�A�G���[�l
#NUM!���Ԃ���܂��BA�����B���ȗ�����ƁA�W���ݐσ����z���g�p����AA =
0 ����� B = 1 �Ƃ��Čv�Z���s���܂��B�v�Z�ɂ́A���x���}3x10-7�ȓ��ɂȂ�܂Ŕ����v�Z�̎�@���g�p�����̂ŁA�����v�Z��100��s���Ă����ʂ��������Ȃ��ꍇ�́A�G���[�l #N/A ���Ԃ���܂��B
�g�p��
���BETADIST���ŋ��߂��m�����t�Z����ƁA�w�͂S�D�X�X�X�X�W�ł��邱�Ƃ����߂��܂��B�T�ɂȂ�Ȃ��̂͏����_�ȉ��̌����ɂ��v�Z���x�ɂ��B
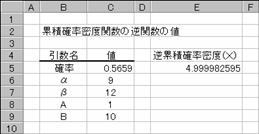 �@EX4A179Z
�@EX4A179Z
E5
:=BETAINV(C5,C6,C7,C8,C9)
�y�܂Ƃ߁z
BETADIST �ݐϊm�����x�̒l��Ԃ��܂��B
BETAINV �ݐϊm�����x�̋t���̒l��Ԃ��܂��B
�����z
���z�ɊW������ɂ́ABINOMDIST���ACRITBINOM���ANEGBINOMDIST���APERMUT���APROB���AHYPGEOMDIST���A������܂��B
BINOMDIST�� ���z�̊m��
CRITBINOM�� �ݐϓ��z�̍ŏ��̒l
NEGBINOMDIST�� ���̓��z
PERMUT�� �W�{���̏���
PROB�� �����Ə���Ԃ̊m��
HYPGEOMDIST�� �����z���̒l
���a�h�m�n�l�c�h�r�s��
�ʍ��̓��z�̊m����Ԃ��܂��B���Ƃ��A�R�C���𓊂������ʁA�\���o�邩�A�����o�邩�̓�ґ���̊m�������߂邱�Ƃ��ł��܂��B���߂�m���͎��̏����ɓ��Ă͂܂錻�ۂ������ɂȂ�܂��B
���s�̌��ʂ������܂��͎��s�̂����ꂩ�ł���
���s���Ɨ��������̂ł���
������ʂ��Đ����̊m�������ł���
���� BINOMDIST(������, ���s��, ������, ���`��)
������ ���s�Ɋ܂܂�鐬���̉��w�肵�܂��B
���s�� ���s�̉��w�肵�܂��B
������ 1��̎��s����������m�����w�肵�܂��B
���`�� �v�Z���@��_���l�Ŏw�肵�܂��B
�_���l ���@
TRUE �ݐϕ��z���Ōv�Z����
FALSE �m�����x���Ōv�Z����
�������A���s�ɐ����Ŏw�肷��i�����_�ȉ��͐�̂Ă���j�B������<0�܂��͐�����>���s�ł���ꍇ�A���邢�͐����� < 0 �܂��� ������ > 1 �ł���ꍇ�A�G���[�l #NUM! ���Ԃ���܂��B�m�����x���́A���̐����ŕ\����܂��B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A056Z
������
�@�@�@�@�@�@�@�@�@�@ EX4A057Z
�� COMBIN(n,x) ��\���܂��B
�ݐϕ��z���́A���̐����ŕ\����܂��B
EX4A058Z
�g�p��
�}�`�́A�R�C���𓊂������ʂ́A�\���o�邩�A�����o�邩�̊m�������߂Ă��܂��B�R�C����1���ĕ\���o��m����0.5�Ƃ��āA10���ĕ\���W��o��m�������߂Ă��܂��B
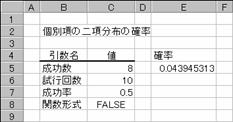 �@EX4A180Z
�@EX4A180Z
E5
:=BINOMDIST(C5,C6,C7,C8)
���b�q�h�s�a�h�m�n�l��
�ݐϓ��z�̒l����l�ȏ�ɂȂ�悤�ȍŏ��̒l��Ԃ��܂��B���̊��ł́A���i�̐��Y���C���Ń��b�g�S�̂ŋ��e�ł��錇�ו��i���̍ő�l�����肷�邱�Ƃ��ł��܂��B
���� CRITBINOM(���s��, ������, ��)
���s�� �x���k�[�C���s�̉��w�肵�܂��B
������ 1 ��̎��s����������m�����w�肵�܂��B
�� ��l���w�肵�܂��B
���s�ɐ����ȊO�̒l���w�肷��Ə����_�ȉ�����̂Ă��܂��B���s��<0�ł���ꍇ�A���邢�͐����� <= 0 �܂��� ������ >=
1�ł���ꍇ�A���邢�� �� < 0 �܂��� �� > 1�ł���ꍇ�A�G���[�l
#NUM! ���Ԃ���܂��B
�g�p��
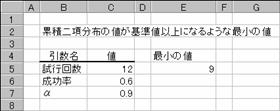 �@EX4A181Z
�@EX4A181Z
E5 :=CRITBINOM(C5,C6,C7)
���g�x�o�f�d�n�l�c�h�r�s��
�����z���̒l��Ԃ��܂��B�w�肳�ꂽ�W�{���A��W�c�̐������A��W�c�̑傫������A��萔�̕W�{����������m�����v�Z���܂��B
���� HYPGEOMDIST(�W�{�̐�����, �W�{��, ��W�c�̐�����, ��W�c�̑傫��)
�W�{�̐����� �W�{���Ő������鐔���w�肵�܂��B
�W�{�� �W�{�����w�肵�܂��B
��W�c�̐����� ��W�c���Ő������鐔���w�肵�܂��B
��W�c�̑傫�� ��W�c�S�̂̐����w�肵�܂��B
�����z�͎��̎��ŗ^�����܂��B
EX4A082Z
x = �W�{�̐�����
n = �W�{��
M = ��W�c�̐�����
N = ��W�c�̑傫��
�g�p��
���X�X�̃C�x���g�Œ��I����s�����ƂɂȂ�܂����B�����T�{�A�P���P�O�{�A�Q���Q�O�{�A�R���U�T�{�A�̌v�P�O�O�{�̂����������Œ��I�������Ȃ��܂��B����l���P��̒��I���s���܂����B���̐l���e���Ă�m���͐}�`�̂悤�Ɍv�Z�ł��܂��B�m�������ŕ\������ꍇ�̓Z���f�T�F�f�W�̕\���`�������X�^�C���ɐݒ肵�܂��B�e�����̈Ӗ��͈ȉ��̂Ƃ���ł��B�i���̗�ł͒��I���s�����ƂɈ����̒l���ω����邱�Ƃ��l�����Ă��܂���j
�W�{�̐����� ��� ���I����{��
�W�{�� ��� ���I���s����
��W�c�̐����� ��� �����肭���̐�
��W�c�̑傫�� ��� �����S�̂̐�
�}�`
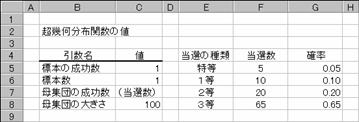 �@EX4A182Z
�@EX4A182Z
G5
:=HYPGEOMDIST($C$5,$C$6,F5,$C$8)
G6
:=HYPGEOMDIST($C$5,$C$6,F6,$C$8)
G7
:=HYPGEOMDIST($C$5,$C$6,F7,$C$8)
G8
:=HYPGEOMDIST($C$5,$C$6,F8,$C$8)
���m�d�f�a�h�m�n�l�c�h�r�s��
���̓��z��Ԃ��܂��B���s�̐����������̂Ƃ��A�������Ŏw�肵���̎��s����������O�ɁA���s���Ŏw�肵���̎��s�����s����m�����v�Z�ł��܂�
���� NEGBINOMDIST(���s��, ������, ������)
���s�� ���s�����s������w�肵�܂��B
������ ���s������������w�肵�܂��B
������ ���s����������m�����w�肵�܂��B
���s���A�������ɏ����_�ȉ��̒l���w�肵�Ă���̂Ă��܂��B������<=0�A�܂��͐�����>= 1�ł���ꍇ�A���邢��(���s��+������-1)<=0�ł���ꍇ�A�G���[�l#NUM!���Ԃ���܂��B���̓��z�͎��̂悤�ɒ�`����܂��B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A093Z
x = ���s��
r = ������
p = ������
�g�p��
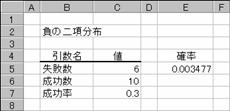 �@EX4A183Z
�@EX4A183Z
E5
:=NEGBINOMDIST(C5,C6,C7)
���o�d�q�l�t�s��
�W�{�����甲����萔��I������ꍇ�̏����Ԃ��܂��B
���� PERMUT(�W�{��, ������萔)
�W�{�� �Ώۂ̑����𐮐��Ŏw�肵�܂��B
������萔 �Ώۂ̌��𐮐��Ŏw�肵�܂��B
�����ɏ����_�ȉ��̒l���w�肵�Ă���̂Ă��܂��B�W�{���A������萔�ɐ��l�ȊO�̒l���w�肷��ƁA�G���[�l#VALUE!���Ԃ���܂��B�W�{������0�܂��͔�����萔<0�̏ꍇ�A�W�{��<������萔�ł���ꍇ�A�G���[�l #NUM! ���Ԃ���܂��B����͎��̎��Ōv�Z����܂��B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A097Z
�g�p��
�ԍ����P�`�T�̐����R�����ׂ��ꍇ�A�g�ݍ��킹����̑����͐}�`�̂悤�Ɍv�Z�ł��܂��B
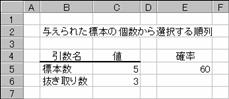 �@EX4A184Z
�@EX4A184Z
E5 :=PERMUT(C5,C6)
���o�q�n�a��
x�͈͂Ɋ܂܂��l�������Ə���Ƃ̊ԂɎ��܂�m����Ԃ��܂��B
���� PROB(x�͈�, �m���͈�, ����, ���)
x�͈� �m���͈͂ƑΉ��W�ɂ��鐔�lx���܂ރZ���͈͂��w�肵�܂��B
�m���͈� x�͈͂Ɋ܂܂�邻�ꂼ��̐��l�ɑΉ�����m�����w�肵�܂��B
���� �ΏۂƂȂ鐔�l�̉������w�肵�܂��B
��� �ΏۂƂȂ鐔�l�̏�����w�肵�܂��i�ȗ��j
������ȗ�����ƁAx�͈͂Ɋ܂܂��l�������Ɠ������Ȃ�m�����v�Z����܂��B
�m���͈͂Ɋ܂܂��l��0�����܂���1����Ƃ��A�m���͈͂Ɋ܂܂��l�̍��v��1�ɂȂ�Ȃ��Ƃ��A�G���[�l #NUM! ���Ԃ���܂��Bx�͂Ɗm���͈͂̃f�[�^�̌����قȂ�ƁA�G���[�l #N/A ���Ԃ���܂��Bx�͈͂Ɗm���͈͔͂z��萔�Ŏw�肷�邱�Ƃ��ł���B
�g�p��
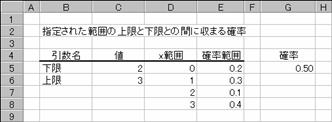 �@EX4A185Z
�@EX4A185Z
G5
:=PROB(D5:D8,E5:E8,C5,C6)
�y�܂Ƃ߁z
BINOMDIST �ʍ��̓��z�̊m����Ԃ��܂��B
CRITBINOM �ݐϓ��z�̒l����l�ȏ�ɂȂ�悤�ȍŏ��̒l��Ԃ��܂��B
HYPGEOMDIST �����z���̒l��Ԃ��܂��B
NEGBINOMDIST ���̓��z��Ԃ��܂��B
PERMUT �^����ꂽ�W�{�̌�����w�肵������I������ꍇ�̏����Ԃ��܂��B
PROB �w�肳�ꂽ�͈͂Ɋ܂܂��l������Ɖ����Ƃ̊ԂɎ��܂�m����Ԃ��܂��B
���J�C2��
�J�C 2 ������߂���͎��̂R������܂��B
CHIDIST�� �Б��J�C2��(��2)���z�̊m��
CHIINV�� �J�C2��(��2)���z�̋t��
CHITEST�� �J�C2��(��2)����
���b�g�h�c�h�r�s��
�Б��J�C2��(��2)���z�̊m����Ԃ��܂��B
���� CHIDIST(x, ���R�x)
x ���z��]������l���w�肵�܂��B
���R�x ���R�x���w�肵�܂��B
����x�ɕ��̐����w�肷��ƁA�G���[�l #NUM! ���Ԃ���܂��B���R�x�ɐ����ȊO�̒l���w�肷��ƁA�����_�ȉ�����̂Ă��܂��B���R�x<1�܂��͎��R�x=>1010�ł���ꍇ�A�G���[�l #NUM! ���Ԃ���܂��B
���b�g�h�h�m�u��
�J�C2�� (��2)���z�̋t����Ԃ��܂��B
���� CHIINV(�m�� ���R�x)
�m�� ��2���z�ɔ����m�����w�肵�܂��B
���R�x ���R�x���w�肵�܂��B
���R�x �ɐ����ȊO�̒l���w�肷��ƁA�����_�ȉ�����̂Ă��܂��B�m��<0�܂��͊m��>1�ł���ꍇ�A ���R�x<1�܂��͎��R�x����1010�ł���ꍇ�A�G���[�l
#NUM! ���Ԃ���܂��B�v�Z���ʂ̐��x���}3�d-7�ȓ��ɂȂ�܂Ŕ����v�Z���s���A�����v�Z��100��s���Ă����ʂ��������Ȃ��ꍇ�́A�G���[�l#N/A ���Ԃ���܂��B
�g�p��
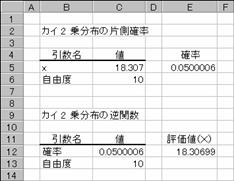 �@EX4A186Z
�@EX4A186Z
E5 :=CHIDIST(C5,C6)
E12:=CHIINV(C12,C13)
���b�g�h�s�d�r�s��
�J�C2��(��2)������s���܂��B
���� CHITEST(�����l�͈�, ���Ғl�͈�)
�����l�͈� ����̎����l�����͂���Ă���f�[�^�͈͂��w�肵�܂��B
���Ғl�͈� ���Ғl�����͂���Ă���f�[�^�͈͂��w�肵�܂��B
�����l�Ɗ��Ғl�ł́A�s�����̒l�̍��v�Ɨ�����̒l�̍��v�����ꂼ�ꓙ�����Ȃ��Ă���K�v������܂��B�����l�͈͂Ɗ��Ғl�͈͂Ɋ܂܂��f�[�^�̌����قȂ�ꍇ�A�G���[�l #N/A ���Ԃ���܂��B��2����ł́A�܂���2���v�ʂ��v�Z����A���Ɏ����l�Ɗ��Ғl�̍������Z����܂��B�v�Z�l�͓���CHITEST=p(X>��2)�ŕ\����܂��B��2���v�ʂƎ��R�xdf�ɑ���m�����v�Z����܂��B���̂Ƃ��Adf = (r-1)(c-1) �ƂȂ�܂��B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A059Z
Aij = i �s j ����̎����l�̓x��
(�����l�p�x)
Eij = i �s j ����̊��Ғl�̓x��
(���Ғl�p�x)
r = �s��
c = ��
�g�p��
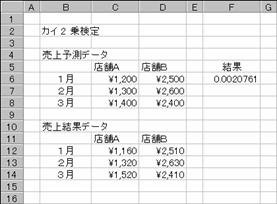 EX4A187Z
EX4A187Z
F6
:=CHITEST(C12:D14,C6:D8)
�y�܂Ƃ߁z
CHIDIST �J�C 2 �敪�z�̕Б��m����Ԃ��܂��B
CHIINV �J�C 2 �敪�z�̋t���̒l��Ԃ��܂��B
CHITEST �J�C 2 �挟����s���܂��B
���W�{�̕��ϒl�ɑ�����̕����a
�W�{�̕��ϒl�ɑ���e�f�[�^�̕��̕����a��Ԃ��܂��B
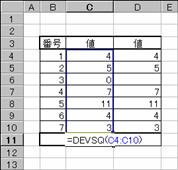
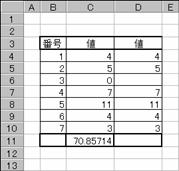
���� DEVSQ(���l1, ���l2, ...)
���l1,���l2,... ���̕����a�����߂鐔�l���w�肷��i�ő�R�O�܂Łj
���̕����a�́A���̐����ŕ\����܂��B
![]() EX4A565Z
EX4A565Z
�g�p��
�m�`�n��������͂���
�m�a�n����
 �@�@
�@�@
EX4A566Z�@�@�@�@�@�@�@�@�@�@�@�@EX4A567Z
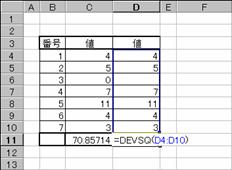
�m�b�n��������͂���
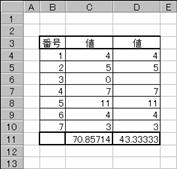
�m�c�n�Z�����܂ޏꍇ�̌���
 |
 �@�@
�@�@
EX4A568Z�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A569Z
�쐬�菇
�@���āA�ǂ����珑���n�߂�����̂ł��傤�B

 |