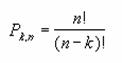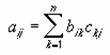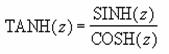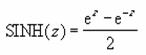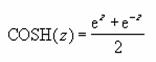3-3 ���w�O�p���i���l�̌v�Z�j
�@
![]()
�@�@ �Q�Q�Q
���O�p��
�w�肵���p�x�̃T�C���l��R�T�C���l�A���邢�̓^���W�F���g�l�����߂�ɂ́ASIN���ACOS���ATAN�����g���܂��B
���� SIN(���l) �w�肵���p�x�̃T�C���l��Ԃ�
COS(���l) �w�肵���p�x�̃R�T�C���l��Ԃ�
TAN(���l) �w�肵���p�x�̃^���W�F���g�l��Ԃ�
�����i���l�j�́A�v�Z����p�x�i���l�j�����W�A���P�ʂŎw�肷��B�p�x���x�i�f�W�A���j��P�ʂƂ��ĕ\����Ă���ꍇ�́API()/180 �������ă��W�A���ɕϊ��A���邢�͊p�x�ϊ������g���ϊ������l�Ŏw�肷��B���W�A���͉~�����O�`�U�D�Q�W�i�Q�j�ŕ\���l�̂��Ƃł��B���߂��l�������̏ꍇ�͍����i�����v�����j�A�����̏ꍇ�͉E���i���v�����j��\����B
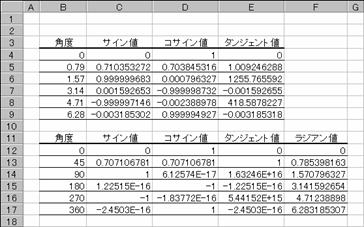
�g�p��
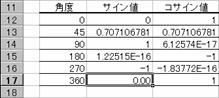
���̗�́A�p�x�ɑ���T�C���A�R�T�C���A�^���W�F���g�l�����߂Ă��܂��B�}���̏㑤�ł́A���W�A���l�����Ɍv�Z���āA�����ł͊p�x��RADIANS���Ń��W�A���l�ɕϊ������l�Ōv�Z����悤�ɂ��Ă��܂��B�Z���b�P�T�i���߂��l-2.4503E-16�j�̂悤�ɔ��ɏ������l�̓[���̋ߎ��l�ɂȂ�܂��B
|
|
�@�@�@�@�@1.57
 |
3.14�@�@�@�@�@�@�@�@�@�@�@�@�@�@0
![]()
�@6.28=0
4.71
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A130Z
C4:=SIN(B4) D4:=COS(B4) E4:=TAN(B4)
C5:=SIN(B5) C5:=COS(B5) C5:=TAN(B5)
C6:=SIN(B6) C6:=COS(B6) C6:=TAN(B6)
C7:=SIN(B7) C7:=COS(B7) C7:=TAN(B7)
C8:=SIN(B8) C8:=COS(B8) C8:=TAN(B8)
C9:=SIN(B9) C9:=COS(B9) C9:=TAN(B9)
C12:=SIN(RADIANS(B12)) D12:=COS(RADIANS(B12)) E12:=TAN(RADIANS(B12))
C13:=SIN(RADIANS(B13)) D13:=COS(RADIANS(B13)) E13:=TAN(RADIANS(B13))
C14:=SIN(RADIANS(B14)) D14:=COS(RADIANS(B14)) E14:=TAN(RADIANS(B14))
C15:=SIN(RADIANS(B15)) D15:=COS(RADIANS(B15)) E15:=TAN(RADIANS(B15))
C16:=SIN(RADIANS(B16)) D16:=COS(RADIANS(B16)) E16:=TAN(RADIANS(B16))
C17:=SIN(RADIANS(B17)) D17:=COS(RADIANS(B17)) E17:=TAN(RADIANS(B17))
F12:=RADIANS(B12)
F13:=RADIANS(B13)
F14:=RADIANS(B14)
F15:=RADIANS(B15)
F16:=RADIANS(B16)
F17:=RADIANS(B17)
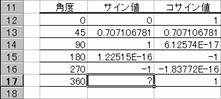
�����߂��l���u�H�v�ɂȂ�
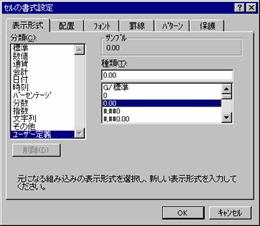
�����_�ȉ��̌�����ύX���邽�߂ɁA�c�[���o�[�́m�����_�\�����グ�n�m�����_�\���������n�{�^�����N���b�N����Ɓu�H�v�i�}�`�j�ɕς�邱�Ƃ�����܂��B���̌��ۂ̓Z���̕\���`���ɖ�肪����܂��B
 �@EX4A131Z
�@EX4A131Z
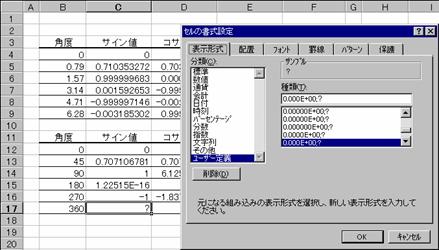
�l�ł͂Ȃ��u�H�v���\�����ꂽ�Z�����E�N���b�N���ăV���[�g�J�b�g���j���[�́m�Z���̏����ݒ�n��I�����ĕ\���`�������Ă��������B��ނ̗��Ɂu�O�D�O�O�O�d�{�O�O�G�H�v���\������Ă��܂��B���̌`���̃[���\���̕����ɁH�����͂���Ă���̂ŁA�[���A���邢�͔��Ƀ[���ɋ߂��l�̂Ƃ��A�u�H�v���\�������̂ł��B�u�H�v�ł͂Ȃ��u�O�v��\��������ꍇ�A�\���`���ɂO�D�O�O��I����������B�`�����O�D�O�O�ɐ݂���A�c�[���o�[�́m�����_�\�����グ�n�m�����_�\���������n�{�^���Ō�����C�ӂɕύX���邱�Ƃ��ł��܂��B
�r������
�m�`�n�ύX����Z����I�����ām�Z���̏����ݒ�n�_�C�A���O�{�b�N�X���J��
�@�m�\���`���n�^�u���N���b�N����
�m�a�n���݂̕\���`�����\�������
�A�ꗗ���̂O�D�O�O��I������
�B�m�n�j�n���N���b�N����
�m�b�n�l���\�������
���ށm���[�U�[�ݒ�n�ɂO�D�O�O����������Ȃ��Ƃ��́A���͗��i�}�m�a�n�j�ɒ��ړ��͂��Ă��������B
 |
 �@EX4A132Z
�@EX4A132Z
 �@�@�@�@�@�@�@
�@�@�@�@�@�@�@
EX4A133Z�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A139Z
�y�܂Ƃ߁z
SIN ���l�̃T�C����Ԃ���B
COS ���l�̃R�T�C����Ԃ���B
TAN ���l�̃^���W�F���g��Ԃ���B
���t�O�p��
���l�̋t�O�p���i�t�O�p�̂��Ƃ��A�[�N�Ƃ����j�A�A�[�N�T�C���A�A�[�N�R�T�C���A�A�[�N�^���W�F���g�A�����߂��������܂��B
���`�b�n�r��
���l�̃A�[�N�R�T�C����Ԃ���B�߂�l�̊p�x�́A0(�[��)�`��(�p�C)�͈̔͂̃��W�A���ŕԂ���܂��B
���� ACOS(���l)
���l ���߂�p�x�̃R�T�C���̒l���A-1 �` 1�͈̔͂Ŏw�肷��
���`�r�h�m��
���l�̃A�[�N�T�C����Ԃ���B�߂�l�̊p�x�́A-��/2�`��/2�͈̔͂̃��W�A���ŕԂ���܂��B
���� ASIN(���l)
���l ���߂�p�x�̃T�C���̒l���A-1�`1�͈̔͂Ŏw�肷��
���`�s�`�m��
���l�̃A�[�N�^���W�F���g��Ԃ���B�߂�l�̊p�x�́A-��/2�`��/2�͈̔͂̃��W�A���ŕԂ���܂��B
���� ATAN(���l)
���l ���߂�p�x�̃^���W�F���g�̒l���w�肷��B
�t�O�p���̒l��x�ŕ\���ɂ́A�v�Z���ʂ�180/PI()���|����A���邢�͂c�d�f�q�d�d�r���œx�ɕϊ����܂��B180/PI()���g�����v�Z������͂����Ƃ��A�Z���ɁH���\�����ꂽ�ꍇ�A�\���`����K�ɐݒ肵�����Ă��������B�i�ڍׂ͂o�Q�Q�Q�Q�Ɓj
�g�p��
�}�`�̓��W�A���Ŏw�肷��p�x�ɑ���t�O�p���̒l�ƁA���߂��l��x�ɕϊ������l�����߂Ă��܂��B
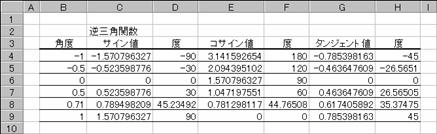 �@EX4A134Z
�@EX4A134Z
���͂��鐔��
C4 =ASIN(B4) D4 =DEGREES(C4)
C5 =ASIN(B5) D5 =DEGREES(C5)
C6 =ASIN(B6) D6 =DEGREES(C6)
C7 =ASIN(B7) D7 =DEGREES(C7)
C8 =ASIN(B8) D8 =DEGREES(C8)
C9 =ASIN(B9) D9 =DEGREES(C9)
E4 =ACOS(B4) F4 =DEGREES(E4)
E5 =ACOS(B5) F5 =DEGREES(E5)
E6 =ACOS(B6) F6 =DEGREES(E6)
E7 =ACOS(B7) F7 =DEGREES(E7)
E8 =ACOS(B8) F8 =DEGREES(E8)
E9 =ACOS(B9) F9 =DEGREES(E9)
G4 =ATAN(B4) H4 =DEGREES(G4)
G5 =ATAN(B5) H5 =DEGREES(G5)
G6 =ATAN(B6) H6 =DEGREES(G6)
G7 =ATAN(B7) H7 =DEGREES(G7)
G8 =ATAN(B8) H8 =DEGREES(G8)
G9 =ATAN(B9) H9 =DEGREES(G9)
�y�܂Ƃ߁z
ASIN,ACOS,ATAN
* ACOS ���l�̃A�[�N�R�T�C����Ԃ���B
* ASIN ���l�̃A�[�N�T�C����Ԃ���B
* ATAN ���l�̃A�[�N�^���W�F���g��Ԃ���B
���n�C�p�[�{���b�N�O�p��
���l�̑o�Ȑ����i�n�C�p�[�{���b�N�j�A�n�C�p�[�{���b�N�T�C���A�n�C�p�[�{���b�N�R�T�C���A�n�C�p�[�{���b�N�^���W�F���g�A�����߂��������܂��B
��SINH��
���l�̑o�Ȑ����� (�n�C�p�[�{���b�N �T�C��) ��Ԃ�
���� SINH(���l)
���l �o�Ȑ����������߂鐔�l���w�肷��B
�o�Ȑ����� (�n�C�p�[�{���b�N �T�C��) �͎��̐����Ōv�Z����܂��B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ EX4A123Z
�����̎w��ł���͈͂́A�v�Z���ʂ��L�������͈͓��܂ʼn\�ł��B���ʂ��I�[�o�[�t���[�i�L���������z����l�j�̂Ƃ�#NUM!���\������܂��B
��COSH��
���l�̑o�Ȑ��]�� (�n�C�p�[�{���b�N �R�T�C��) ��Ԃ���B
���� COSH(���l)
�o�Ȑ��]���́A���̐����ŕ\����܂��B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A054Z
��TANH��
���l�̑o�Ȑ�����(�n�C�p�[�{���b�N �^���W�F���g) ��Ԃ���B
���� TANH(���l)
���l �������w�肷��B
�o�Ȑ����ڂ́A���̐����ŕ\����܂��B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A127Z
�g�p��
�}�`�̓��W�A���Ŏw�肷��p�x�ɑ���o�Ȑ����̒l�����߂Ă��܂��B�Ȃ��A���߂��l��x�ɕϊ�����ꍇ�́A�v�Z���ʂ�180/PI()���|����A���邢�͂c�d�f�q�d�d�r���œx�ɕϊ����܂��B
�}�`
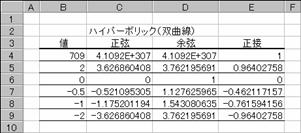 �@EX4A135Z
�@EX4A135Z
�b�S�@���r�h�m�g�i�a�S�j �c�S�@���b�n�r�g�i�a�S�j �d�S�@���s�`�m�g�i�a�S�j
�b�T�@���r�h�m�g�i�a�T�j �c�S�@���b�n�r�g�i�a�T�j �d�S�@���s�`�m�g�i�a�T�j
�b�U�@���r�h�m�g�i�a�U�j �c�S�@���b�n�r�g�i�a�U�j �d�S�@���s�`�m�g�i�a�U�j
�b�V�@���r�h�m�g�i�a�V�j �c�S�@���b�n�r�g�i�a�V�j �d�S�@���s�`�m�g�i�a�V�j
�b�W�@���r�h�m�g�i�a�W�j �c�S�@���b�n�r�g�i�a�W�j �d�S�@���s�`�m�g�i�a�W�j
�b�X�@���r�h�m�g�i�a�X�j �c�S�@���b�n�r�g�i�a�X�j �d�S�@���s�`�m�g�i�a�X�j
�y�܂Ƃ߁z
SINH,COSH,TANH
* COSH ���l�̃n�C�p�[�{���b�N �R�T�C����Ԃ���B
* TANH ���l�̃n�C�p�[�{���b�N �^���W�F���g��Ԃ���B
* SINH ���l�̃n�C�p�[�{���b�N �T�C����Ԃ���B
���n�C�p�[�{���b�N�t�O�p��
���l�̑o�Ȑ��t���i�n�C�p�[�{���b�N�A�[�N�j�A�n�C�p�[�{���b�N�A�[�N�T�C���A�n�C�p�[�{���b�N�A�[�N�R�T�C���A�n�C�p�[�{���b�N�A�[�N�^���W�F���g�A�����߂��������܂��B
��ACOSH��
���l�̑o�Ȑ��t�]�� (�n�C�p�[�{���b�N �R�T�C���̋t��) ��Ԃ���B
���� ACOSH(���l)
���l 1 �ȏ�̎������w�肷��B
��ASINH��
���l�̑o�Ȑ��t���� (�n�C�p�[�{���b�N �T�C���̋t��) ��Ԃ���B
���� ASINH(���l)
���l �������w�肷��B
��ATANH��
���l�̑o�Ȑ��t���ځi�n�C�p�[�{���b�N �^���W�F���g�̋t���j��Ԃ���B
���� ATANH(���l)
���l -1���傫��1��菬�����������w�肷��B
�g�p��
�G���[���m�t�l�I�͌v�Z�s�\��\���Ă��܂��B�l�ɑ��錋�ʂ��Ȃ��Ƃ������Ƃł��B
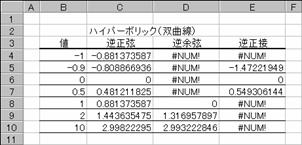 �@EX4A136Z
�@EX4A136Z
�b�S�@�@���`�r�h�m�g�i�a�S�j �c�S�@�@���`�b�n�r�g�i�a�S�j �d�S�@�@���`�s�`�m�g�i�a�S�j
�b�T�@�@���`�r�h�m�g�i�a�T�j �c�S�@�@���`�b�n�r�g�i�a�T�j �d�S�@�@���`�s�`�m�g�i�a�T�j
�b�U�@�@���`�r�h�m�g�i�a�U�j �c�S�@�@���`�b�n�r�g�i�a�U�j �d�S�@�@���`�s�`�m�g�i�a�U�j
�b�V�@�@���`�r�h�m�g�i�a�V�j �c�S�@�@���`�b�n�r�g�i�a�V�j �d�S�@�@���`�s�`�m�g�i�a�V�j
�b�W�@�@���`�r�h�m�g�i�a�W�j �c�S�@�@���`�b�n�r�g�i�a�W�j �d�S�@�@���`�s�`�m�g�i�a�W�j
�b�X�@�@���`�r�h�m�g�i�a�X�j �c�S�@�@���`�b�n�r�g�i�a�X�j �d�S�@�@���`�s�`�m�g�i�a�X�j
�b�P�O�@���`�r�h�m�g�i�a�P�O�j �c�P�O�@���`�b�n�r�g�i�a�P�O�j �d�P�O�@���`�s�`�m�g�i�a�P�O�j
�y�܂Ƃ߁z
* ACOSH ���l�̃n�C�p�[�{���b�N �A�[�N�R�T�C����Ԃ���B
* ASINH ���l�̃n�C�p�[�{���b�N �A�[�N�T�C����Ԃ���B
* ATANH ���l�̃n�C�p�[�{���b�N �A�[�N�^���W�F���g��Ԃ���B
��x-y���W�̃A�[�N�^���W�F���g
�w�肷��(x,y)���W�̃A�[�N�^���W�F���g��ATAN2���ŋ��߂܂��B�A�[�N�^���W�F���g�́Ax�����猴�_0��(x,y)���W��ʂ钼���̌X���̂��Ƃł��B�߂�l�́A-�`��(������-���Ȃ̂Ł|������)�͈̔͂̃��W�A���l�ɂȂ�܂��B
���� ATAN2(x���W, y���W)
�@x���W �_��x���W���w�肷��
�@y���W �_��y���W���w�肷��
���
�߂�l�����̐��Ȃ�x�����甽���v���̊p�x��\���A���̐��Ȃ�x�����玞�v���̊p�x��\����B�����̌X���i�N���オ��p�x�j��ATAN(Y/X)�ŋ��߂��܂����A�w���O�̏ꍇ�O���Z�G���[�i#DIV/0�j�ɂȂ�v�Z�s�\�ɂȂ�܂��B�������A�w���O�́}�X�O�x�ɂȂ�̂Ōv�Z�s�\�ł͎��p�I�ł���܂���BATAN2���ł́A�w��0���w�肷�邱�Ƃ��ł��܂��B�������Ax��y���W�������Ƃ�0�ł���ꍇ�A�G���[�l#DIV/0���Ԃ���܂��B
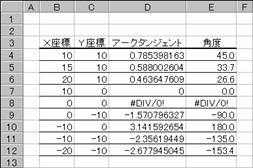
�g�p��
|
|
���̗�́A���_(0,0)����i�w�C�x�j�_��ʂ钼���̋N���オ��p�x�����߂Ă��܂��B�Ԃ����l�̓��W�A���l�ɂȂ�̂ŁA�p�x�Ƃ��ċ��߂�ꍇ�́ADEGREES���i���邢��180/PI()���|����j���g���ēx�ɕϊ�����B
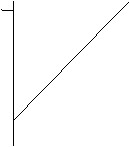 |
�@�@�@�@�@�@�@�@�@�@10
�@�@�@�@�@�@�@�@�@�@
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@45�
�@�@�@�@�@�@�@�@�@�@�@�O �@�@�@�@�@�@�@10
�@EX4A137Z
���͂��鐔��
D4 :=ATAN2(B4,C4) E4 :=DEGREES(D4)
D5 :=ATAN2(B5,C5) E5 :=DEGREES(D5)
D6 :=ATAN2(B6,C6) E6 :=DEGREES(D6)
D7 :=ATAN2(B7,C7) E7 :=DEGREES(D7)
D8 :=ATAN2(B8,C8) E8 :=DEGREES(D8)
D9 :=ATAN2(B9,C9) E9 :=DEGREES(D9)
D10:=ATAN2(B10,C10) E10:=DEGREES(D10)
D11:=ATAN2(B11,C11) E11:=DEGREES(D11)
D12:=ATAN2(B12,C12) E12:=DEGREES(D12)
�y�܂Ƃ߁z
* ATAN2 x-y
���W�̒l����A�[�N�^���W�F���g��Ԃ���B
���~�����Ɗp�x�P�ʂ̊�
�~�����͂R�D�P�S���Ƃ������Ƃ͂悭�m���Ă��邱�Ƃł����A�~������\�������g���ƂP�T���̐��x�ʼn~�������w��ł��܂��B�܂��A�p�x�͂P�����R�U�O�x�Ƃ����P�ʂƂU�D�Q�W�i�Q�j�Ƃ������W�A���Ƃ����P�ʂ�����A���݂ɕϊ������������܂��B
���o�h��
�~�����̋ߎ��l��3.14159265358979��Ԃ���B���̐��l�̐��x��15���ł��B
���� PI()
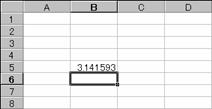
�g�p��
������͂���A���̃Z���Ƀ̒l���\������܂��B�\�������̓Z�����ɂ��܂��B
 �@
�@
EX4A570Z�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A571Z
��DEGREES��
���W�A����x�ɕϊ�����B
���� DEGREES(�p�x)
�p�x �x�ɕϊ�����p�x�i���W�A���l�j���w�肷��B
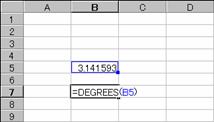
�g�p��
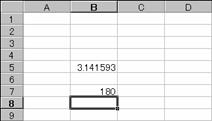
�}�ł̓̒l��x���ɕϊ����Ă��܂��B
�m�`�n������͂���
�m�a�n���ʂ����߂���
 �@
�@
EX4A572Z�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A573Z
��RADIANS��
�x�����W�A���ɕϊ�����B
���� RADIANS(�p�x)
�p�x ���W�A���ɕϊ�����p�x���w�肷��B
�g�p��
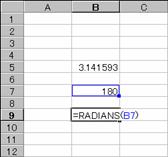
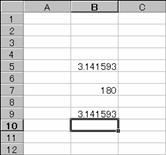
�}�ł́A�x�������W�A���l�ɕϊ����Ă��܂��B
�m�`�n������͂���
�m�a�n���ʂ����߂���
 �@�@
�@�@
EX4A574Z�@�@�@�@�@�@�@�@�@�@�@EX4A575Z
�����ƌ��{��
���l�i�����j�̍ő���ƍŏ����{�������߂��������܂��B�����Q�̊��́A���j���[�m�c�[���n�m�A�h�C���n�Łu���̓c�[���v���Z�b�g�A�b�v���Ă��Ȃ��ƒl�����߂��܂���B
���f�b�c�� �v ���̓c�[��
�����̐����̍ő����Ԃ��B
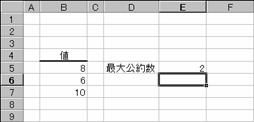
���� GCD(���l1, ���l2, ...)
���l1,���l2,, ... �ő�������߂鐔�l���w�肷��i�ő�R�O�܂Łj
�����ɏ����_�ȉ��̒l���w�肷��Ɛ�̂Ă��܂��B�����ɕ��̒l���w�肷��ƃG���[�l#NUM!���Ԃ���܂��B
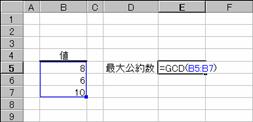
�g�p��
�m�`�n��������͂���
�m�a�n����
 �@�@
�@�@
EX4A576Z�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A577Z
��LCM�� �v ���̓c�[��
�����̐����̍ŏ����{����Ԃ��B
���� LCM(���l1, ���l2, ...)
���l1, ���l2,... �ŏ����{�������߂鐔�l���w�肷��i�ő�R�O�܂Łj
�����ɏ����_�ȉ��̒l���w�肷��Ɛ�̂Ă��܂��B�����ɕ��̐����w�肷��ƃG���[�l#NUM!���Ԃ���܂��B
�g�p��
�m�`�n��������͂���
�m�a�n����
 �@
�@
EX4A578Z�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A579Z
���ΐ�
���l�̑ΐ��ɂ́A���R�ΐ����p�ΐ�������A���ꂼ��̒l�����߂��������܂��B�܂��A�ΐ��̋t���Ƃ���e�ׂ̂�������߂��������܂��B
���k�m��
���l�̎��R�ΐ��i�萔e(2.71828182845904)���Ƃ���ΐ��j��Ԃ��BLN����EXP���̋t���ł��B
���� LN(���l)
���l ���R�ΐ������߂鐳�̎������w�肷��B
�g�p��
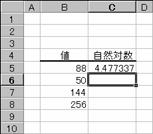
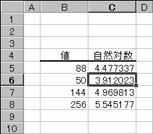
���̗�́A�e�l�̎��R�ΐ������߂Ă��܂��B
�m�`�n��������͂���
�m�a�n���ʂ����߂���
�m�b�n���֑����Z���ɕ��ʂ���
 �@�@
�@�@ �@
�@
EX4A580Z�@�@�@�@�@�@�@�@�@�@EX4A581Z�@�@�@�@�@�@�@�@EX4A582Z
���d�w�o��
e���Ƃ��鐔�l�ׂ̂����Ԃ��B
���� EXP(���l)
���l e���Ƃ���ׂ���̎w�����w�肷��B
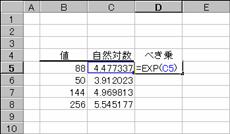
�g�p��
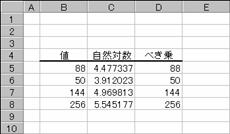
�m�`�n��������͂���
�m�a�n���ʂ����߂���
�m�b�n���֑����Z���ɕ��ʂ���
 �@
�@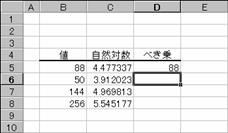
EX4A583Z�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A584Z
 �@EX4A585Z
�@EX4A585Z
���k�n�f��
�w�肳�ꂽ�����Ƃ��鐔�l�̑ΐ���Ԃ��B
���� LOG(���l, ��)
���l �ΐ������߂鐳�̎������w�肷��B
�� �ΐ��̒���w�肷��i�ȗ���10���w�肵���ƌ��Ȃ����j
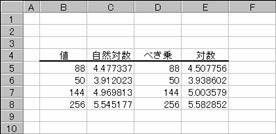
�g�p��
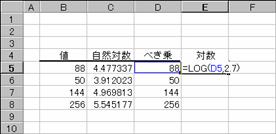
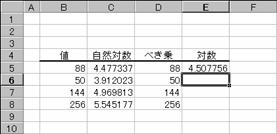
����Q�D�V�ɂ����ΐ�
�m�`�n��������͂���
�m�a�n���ʂ����߂���
�m�b�n���֑����Z���ɕ��ʂ���
 �@
�@
EX4A586Z�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A587Z
 �@EX4A588Z
�@EX4A588Z
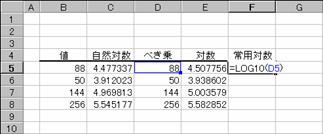
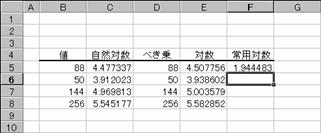
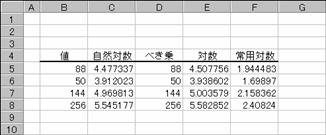
���k�n�f�P�O��
�P�O���Ƃ��鐔�l�̑ΐ��i��p�ΐ��j��Ԃ��B
���� LOG10(���l)
���l �ΐ������߂鐳�̎������w�肷��
�g�p��
�m�`�n��������͂���
�m�a�n���ʂ����߂���
�m�b�n���֑����Z���ɕ��ʂ���
 �@EX4A589Z
�@EX4A589Z
 �@EX4A590Z
�@EX4A590Z
 �@EX4A591Z
�@EX4A591Z
���z��̌v�Z
�����ł����z��Ƃ́A�c���邢�͉��ɘA������Z���ɓ��͂��ꂽ�l�̏W�܂�̂��Ƃ������܂��B���������̓����Z�����̔z��ɑ��āA�������A�����a�A����2��̍��v�A�����߂��������܂��B
���r�t�l�w�Q�l�x�Q��
�Q�̔z��őΉ�����z��v�f�̕����������v����B
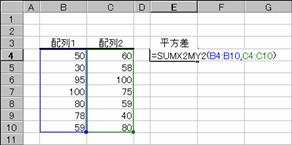
���� SUMX2MY2(�z��1, �z��2)
�z��1 �ΏۂƂȂ����̐��l�z��܂��̓Z���͈͂��w�肷��B
�z��2 �ΏۂƂȂ��������̐��l�z��܂��̓Z���͈͂��w�肷��B
�����Ƃ��Ďw�肵���z���Z���͈͂ɁA������A�_���l�A�܂��͋Z�����܂܂��ꍇ�A�����̒l�͖�������܂��B�z��1�Ɣz��2�̃f�[�^�����قȂ�ƁA�G���[�l#N/A���Ԃ���܂��B�������̍��v�͎��̎��Ōv�Z�ł��܂��B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A124Z
�g�p��
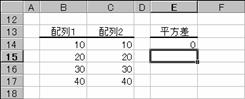
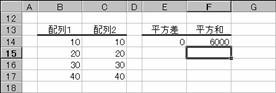
�����f�[�^�̏ꍇ�A���͂Ȃ��̂łO�ɂȂ�
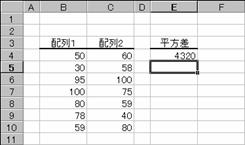
�m�`�n��������͂���
�m�a�n�����������߂���
 �@
�@
EX4A592Z�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A593Z
 �@
�@
EX4A594Z�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A595Z
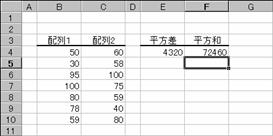
���r�t�l�w�Q�o�x�Q��
2 �̔z��őΉ�����z��v�f�̕����a�����v����B
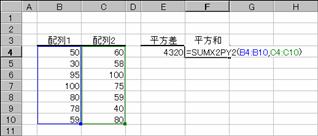
���� SUMX2PY2(�z��1, �z��2)
�z��1 �ΏۂƂȂ����̐��l�z��܂��̓Z���͈͂��w�肷��B
�z��2 �ΏۂƂȂ��������̐��l�z��܂��̓Z���͈͂��w�肷��B
�����Ƃ��Ďw�肵���z���Z���͈͂ɁA������A�_���l�A�܂��͋Z�����܂܂��ꍇ�A�����̒l�͖�������܂��B�z��1�Ɣz��2�̃f�[�^�����قȂ�ƁA�G���[�l#N/A���Ԃ���܂��B�����a�̍��v�͎��̎��Ōv�Z�ł��܂��B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A125Z
�g�p��
�m�`�n��������͂���
�m�a�n�����a�����߂���
 �@
�@
EX4A596Z�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A597Z
 �@
�@
EX4A598Z�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A599Z
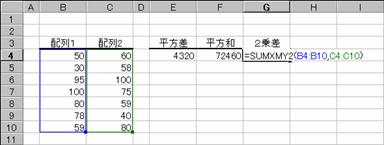
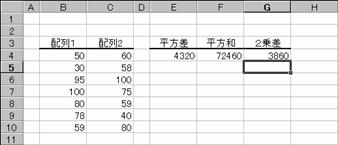
��SUMXMY2��
�Q�̔z��őΉ�����z��v�f�̍����Q�悵�A����ɂ��̍��v��Ԃ��B
���� SUMXMY2(�z��1, �z��2)
�z��1 �ΏۂƂȂ����̐��l�z��܂��̓Z���͈͂��w�肷��B
�z��2 �ΏۂƂȂ��������̐��l�z��܂��̓Z���͈͂��w�肷��B
�����Ƃ��Ďw�肵���z���Z���͈͂ɁA������A�_���l�A�܂��͋Z�����܂܂��ꍇ�A�����̒l�͖�������܂��B�z��1�Ɣz��2�̃f�[�^�����قȂ�ƁA�G���[�l#N/A���Ԃ���܂��B���̊��͎��̎��Ōv�Z����܂��B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A126Z
�g�p��
�m�`�n��������͂���
�m�a�n�����a�����߂���
 �@EX4A602Z
�@EX4A602Z
 �@EX4A603Z
�@EX4A603Z
�����f�[�^�̏ꍇ�A���͂Ȃ��̂łO�ɂȂ�
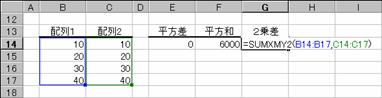 �@EX4A600Z
�@EX4A600Z
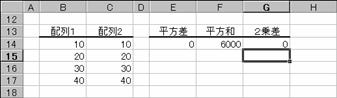 �@EX4A601Z
�@EX4A601Z
������
�s�K���Ȑ��l��ׂɒ��o����l�̂��Ƃ𗐐��Ƃ����܂��B�����͊m���Ȃǂ̃V���~���[�V�����Ȃǂɗ��p����܂��B�����ȉ��̒l��Ԃ����Ɛ�����Ԃ���������܂��B
��RAND��
�O�ȏ�łP��菬���������������܂��B���[�N�V�[�g���Čv�Z����邽�тɁA�V�����������Ԃ���܂��B
���� RAND()
�����Ŕ���������l�ɔ͈͎w�肷��Ƃ��́A���̐������g���܂��B
RAND()*(b-a)+a
���Ƃ��A�T�O�`�P�O�O�͈͓̔��ŗ�����������Ȃ�A�����T�O�A�����P�O�O�Ƃ��āA�ȉ��̂悤�ɂ��܂��B
RAND()*(100-50)+50�@�@�@���@�@RAND()*50+50
�g�p��
���̗�́A�T�O�ȏ�łP�O�O���Ȃ�������������ꍇ�ł��B�����l�͐}�Ɠ����ɂȂ�܂���B
�m�`�n��������͂���
�m�a�n�����l���Ԃ����
�m�b�n�m�e�X�n�L�[�������čČv�Z����Ɨ����l�������ς��
 �@
�@ �@
�@
EX4A604Z�@�@�@�@�@�@�@�@�@�@EX4A605Z�@�@�@�@�@�@�@�@�@EX4A606Z
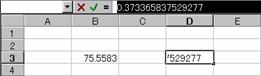
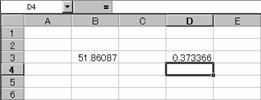
������l�Ƃ��ăZ���ɓ��͂���ꍇ�A�����̓��͂����肷��O�Ɂm�e�X�n�L�[�������čČv�Z���܂��B����Ɛ������l�ɕύX�����̂ŁA�l�Ƃ��ăZ���ɓ��͂��邱�Ƃ��ł��܂��B
�m�`�n�����������鐔������͂���
���m�e�X�n�L�[�������čČv�Z����
�m�a�n���͂����������l�ɏ����ς��
���m�d���������n�L�[�������ē��͌��肷��
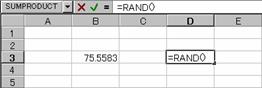
�m�b�n�����ł͂Ȃ��l�����͂��
 |
 �@
�@
EX4A607Z�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A608Z
 �@EX4A609Z
�@EX4A609Z
��RANDBETWEEN�� �v ���̓c�[��
�w�肳�ꂽ�͈͂ň�l�ɕ��z���鐮���̗�����Ԃ��B���[�N�V�[�g���Čv�Z����邽�тɐV�����������Ԃ���܂��B
���� RANDBETWEEN(�ŏ��l, �ő�l)
�ŏ��l �����̍ŏ��l�𐮐��Ŏw�肷��B
�ő�l �����̍ő�l�𐮐��Ŏw�肷��B
�g�p��
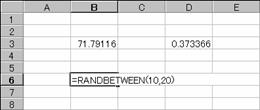
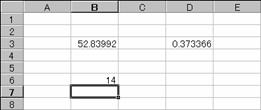
���̗�́A�����l�P�O�`�Q�O�̗��������܂��B
�m�`�n��������͂���
�m�a�n�����l���P�O�`�Q�O�͈͓̔��ŕԂ����
���m�e�X�n�L�[�������čČv�Z����
�m�b�n�����l���P�O�`�Q�O�͈͓̔��ŕԂ����
 �@
�@
EX4A610Z�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A611Z
 �@EX4A612Z
�@EX4A612Z
����Βl
���l�̕������O�����l�̂��Ƃ��Βl�Ƃ����܂��B��Βl�����߂���Ɛ��l�̕��������߂��������܂��B
���`�a�r��
���l�̐�Βl��Ԃ��B��Βl�Ƃ́A���l���畄��(+�A-)���������l�̂��Ƃł��B
���� ABS(���l)
���l ��Βl�����߂�������w�肷��B
�g�p��
�m�`�n��������͂���
�m�a�n�l�̐�Βl�����߂���
�m�b�n���֑����Z���ɐ����ʂ���
 �@
�@ �@
�@
EX4A713Z�@�@�@�@�@�@�@�@�@�@�@�@EX4A714Z�@�@�@�@�@�@�@�@�@�@�@�@EX4A715Z
���r�h�f�m��
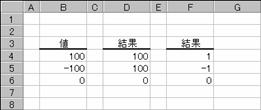
���l�̐����ׂāA���ʂ𐔒l�ŕԂ��܂��B�߂�l�͕\�P�̒ʂ�ł��B
�\�P
�߂�l�@���
�@�P ����
�@�O �O�i���l�̃[���j
�|�P ����
���� SIGN(���l)
���l �����ׂ鐔�l���w�肷��B
�g�p��
�m�`�n��������͂���
�m�a�n���ʂ����߂���
�m�b�n���֑����Z���ɐ����ʂ���
 �@
�@
EX4A716Z�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A717Z
 �@EX4A718Z
�@EX4A718Z
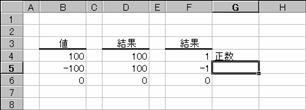
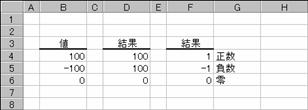
�l�P�O�O�͐����Ȃ̂łP�A�|�P�O�O�͕����Ȃ̂Ł|�P�A�O�̓[���������O�����߂��Ă��܂��B���̗�́A���̌��ʂ𗘗p���Đ����C�����A���\������悤�ɂh�e���Ƒg�ݍ��킹�Ă��܂��B�h�e���͂Q�̏�����I�����铭�������܂����A�ȉ��̂悤�ɂh�e���̒��ɂh�e����g�ݍ��ނ��ƂłQ�ȏ�̏�����I���ł���悤�ɂ��Ă��܂��B
�m�`�n��������͂���
�m�a�n���ʂ����߂���
�m�b�n���֑����Z���ɐ����ʂ���
 �@EX4A720Z
�@EX4A720Z
 �@EX4A721Z
�@EX4A721Z
 �@EX4A719Z
�@EX4A719Z
���ώZ
����l�ƒl���|�����킹��A�K��A��d�K��A�ρA�ׂ���A�����߂��������܂��B�����_�ȉ�����̂Ă���i�����v�Z�j��������̂Œ��ӂ��܂��傤�B
���e�`�b�s��
���l�̊K���Ԃ��B���l�̊K��́A1�`�w�肷�鐔�l�͈̔͂ɂ��鐮���̐ςɂȂ�
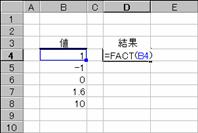
���� FACT(���l)
���l �K������߂鐔�l���w�肷��i�����_�ȉ��͐�̂Ă���j�B
�g�p��
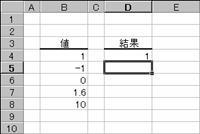
�m�`�n��������͂���
�m�a�n���ʂ����߂���
�m�b�n���֑����Z���ɐ����ʂ���
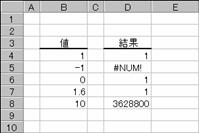
�����͌v�Z�ł��Ȃ��̂ŁA���m�t�l�I�i�Z���c�T�Q�l�j���Ԃ���܂��B
 �@
�@ �@
�@
EX4A722Z�@�@�@�@�@�@�@�@�@�@�@�@EX4A723Z�@�@�@�@�@�@�@�@�@�@�@�@EX4A724Z
���e�`�b�s�c�n�t�a�k�d�� �v ���̓c�[��
���l�̓�d�K���Ԃ��B
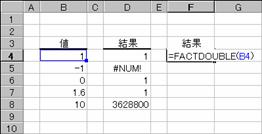
���� FACTDOUBLE(���l)
���l ��d�K������߂鐔�l���w�肷��i�����_�ȉ��͐�̂Ă���j
���l�ɋ������w�肵���ꍇ�́A���̐����Ōv�Z����܂��B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A117Z
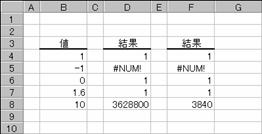
���l�Ɋ���w�肵���ꍇ�́A���̐����Ōv�Z����܂��B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A118Z
�g�p��
�m�`�n��������͂���
�m�a�n���ʂ����߂���
�m�b�n���֑����Z���ɐ����ʂ���
 �@
�@
EX4A725Z�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A726Z
 �@EX4A727Z
�@EX4A727Z
���o�q�n�c�t�b�s��
�������X�g�̐ς�Ԃ��B
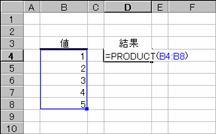
���� PRODUCT(���l1, ���l2, ...)
���l1, ���l2,... �ς��v�Z���鐔�l���w�肷��i�ő�R�O�܂Łj�B
�����̒��Ɋ܂܂�鐔�l�������v�Z�̑ΏۂƂȂ�܂��B�Z���A�_���l�A������A�܂��̓G���[�l�͂��ׂĖ�������܂��B
�g�p��
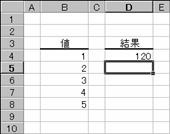
�m�`�n��������͂���
�m�a�n���ʂ����߂���
 �@
�@
EX4A728Z�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A729Z
�����̒��ɕ����������Ă���ꍇ�A�����̐ώZ���s���܂��B�}�b�͕������P�Ȃ̂Ō��ʂ͕����A�}�c�͕������Q�Ȃ̂ŕ����������Ő����ɂȂ��Ă��܂��B
�}�b�@�@�@�@�@�@�@�@�@�@�@�@�@�@�}�c
 �@�@
�@�@
EX4A730Z�@�@�@�@�@�@�@�@�@�@�@EX4A731Z
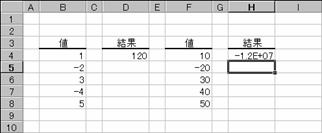
���̗�͌��ʂ̒l���傫���Ȃ�ꍇ�ł��i�}�`�j�B�v�Z���ꂽ���ʂ̌����ɂ��Z����������Ȃ��Ƃ��A�d�L�����g�����d�\�L�ŕ\������܂��i�}�a�j�B�Z������ύX���Ă��Ȃ��ꍇ�ŁA�Ȃ���������ɑ��̃f�[�^�����͂���Ă��Ȃ��ꍇ�A�}�b�̂悤�Ɏ����I�ɃZ��������������Ēʏ�̐��l�ŕ\������܂��B�}�a�̂悤�ɕ\�����ꂽ�Ƃ��ł��A�Z������傫������ΐ}�b�̂悤�ɕ\�������悤�ɂȂ�܂��B
�}�`
 �@EX4A732Z
�@EX4A732Z
�}�a
 �@EX4A733Z
�@EX4A733Z
�}�b
 �@EX4A734Z
�@EX4A734Z
���o�n�v�d�q��
���l�ׂ̂����Ԃ��B���̊��͎Z�p���Z�q�́u�O�v���Z�q�Ɠ������������܂��B
���� POWER(���l, �w��)
���l �ׂ���̒���w�肷��B
�w�� ��Ƃ���ׂ���̎w�����w�肷��B
�g�p��
�m�`�n��������͂���
�m�a�n���ʂ����߂���
 �@
�@
EX4A735Z�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A736Z
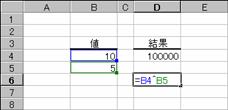
���̗�͉��Z�q�u�O�v���g���Čv�Z���Ă��܂��B
�m�`�n��������͂���
�m�a�n���ʂ����߂���
 �@
�@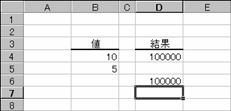
EX4A737Z�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A738Z
���̗�́A���̎w�����w�肵���ꍇ�ł��B
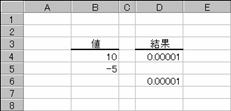 �@EX4A739Z
�@EX4A739Z
���s��
�s��Ƃ͏c�Ɖ��ɘA�������Z���A�܂�A�l�p�`�̗̈�ɒl�����͂���Ă���͈͂̌v�Z�̂��Ƃł��B�ʏ�̍s��v�Z�A�t�s��A�s��ρA�s��ϊ��A���s����������܂��B
���l�c�d�s�d�q�l��
�z��̍s��Ԃ��B
���� MDETERM(�z��)
�z�� �s���Ɨ����������l�z��(�����s��)���w�肷��B
���̊��͎��̐����ŕ\�����Ƃ��ł��܂��B
MDETERM(A1:C3) =
A1*(B2*C3-B3*C2) + A2*(B3*C1-B1*C3) + A3*(B1*C2-B2*C1)
�Ȃ��A�v�Z�͂قڂP�U���̐��x�Ōv�Z����邽�߁A�킸���Ȍ덷�������邱�Ƃ�����܂��B���Ƃ��A���O�ł���Ƃ��A�{���͂O��Ԃ��ׂ��Ƃ����1E-16�̂悤�Ɍ���Ȃ�0�ɋ߂����l�ŕ\�����ꍇ������܂��B
�g�p��
�m�`�n��������͂���
�m�a�n���ʂ����߂���
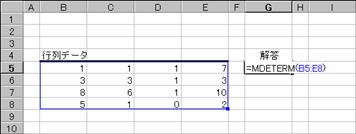 �@EX4A740Z
�@EX4A740Z
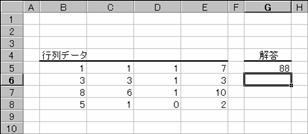 �@EX4A741Z
�@EX4A741Z
���l�h�m�u�d�q�r�d��
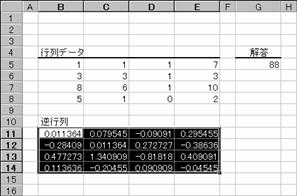
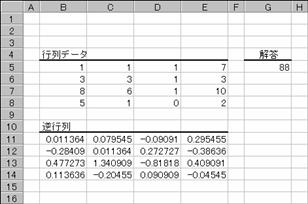
�s��̋t�s���Ԃ��B
���� MINVERSE(�z��)
�z�� �s���Ɨ����������l�z��(�����s��)���w�肷��B
2�s2��̍s��̏ꍇ�A�Z���͈�A1:B2�ɂ͂��ꂼ��a�Ab�Ac�Ad�Ƃ������l�����͂���Ă���Ƃ��A�e�v�f�͎��̂悤�Ɍv�Z����܂��B�Ȃ��A�v�Z�͂قڂP�U���̐��x�Ōv�Z����邽�߁A�킸���Ȍ덷�������邱�Ƃ�����܂��B
�� A �� B
�s 1 d/(a*d-b*c) b/(b*c-a*d)
�s 2 c/(b*c-a*d) a/(a*d-b*c)
�g�p��
�m�`�n���ʂ��o�͂���Z���͈͂�I������
�m�a�n��������͂���
���m�b�s�q�k�n�{�m�r�g�h�e�s�n�{�m�d���������n�L�[������
�m�b�n�z��`���̐��������͂���āA�e�Z���Ɍ��ʂ��\�������
�m�c�n�Z���͈͂̑I���i���]�\���j����������
 �@
�@
EX4A742Z�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A743Z
 �@EX4A744Z
�@EX4A744Z
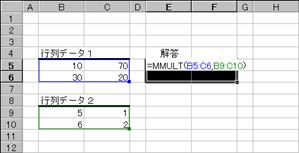
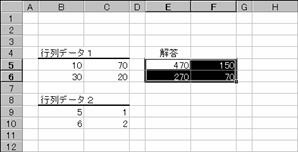
���l�l�t�k�s��
2�̔z��̍s��ς�Ԃ��B�v�Z���ʂ́A�s�����z��1�Ɠ����ŁA���z��2�Ɠ����z��ɂȂ�܂��B
���� MMULT(�z��1, �z��2)
�z��1�A�z��2 �s��ς����߂�2�̔z����w�肷��B
2�̔z��b�Ac�̍s��ςł���z��a�͎��̂悤�ɒ�`����܂��B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A119Z
�����ŁA
i = �s��
j = ��
�g�p��
�m�`�n���ʂ��o�͂���Z���͈͂�I������
�m�a�n��������͂���
���m�b�s�q�k�n�{�m�r�g�h�e�s�n�{�m�d���������n�L�[������
�m�b�n�z��`���̐��������͂���āA�e�Z���Ɍ��ʂ��\�������
�m�c�n�Z���͈͂̑I���i���]�\���j����������
 �@
�@
EX4A745Z�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A746Z
 �@EX4A747Z
�@EX4A747Z
���s�q�`�m�r�o�n�r�d��
�z��̏c�����Ɖ������̃Z���͈͂̕ϊ����s���B���̊��̓��[�N�V�[�g��ɓ��͂����z��f�[�^�̏c�Ɖ����t�]������Ƃ��Ɏg���܂��B
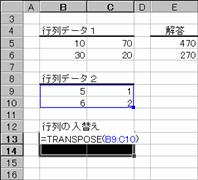
���� TRANSPOSE(�z��)
�z�� �s��ϊ����s���Z���͈͂��w�肵�܂�
�g�p��
�@���ʂ��o�͂���Z���͈͂�I������
�A��������͂���
���m�b�s�q�k�n�{�m�r�g�h�e�s�n�{�m�d���������n�L�[������
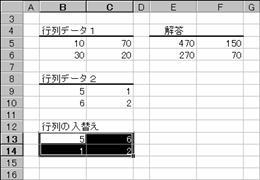
�m�`�n�z��`���̐��������͂���āA�e�Z���Ɍ��ʂ��\�������
�m�a�n�Z���͈͂̑I���i���]�\���j����������
 �@
�@
EX4A748Z�@�@�@�@�@�@�@�@�@�@�@�@EX4A749Z
 �@EX4A750Z
�@EX4A750Z
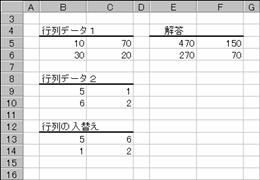
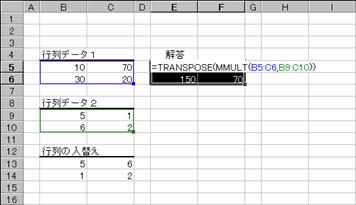
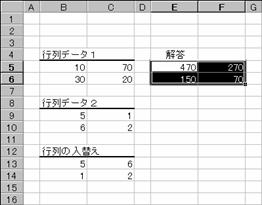
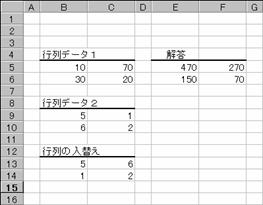
���̗�́A�z���ɑg�ݍ���ŁA�v�Z�̌��ʂ��t�]���Ă��܂��B
�m�`�n�z������͂��Ă���Z���͈͂�I������
���m�e�Q�n�L�[�������Đ����̕ҏW��Ԃɂ���
�@�����������ւ���
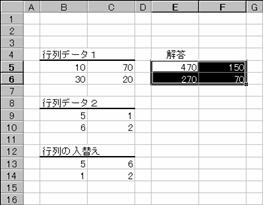
���m�b�s�q�k�n�{�m�r�g�h�e�s�n�{�m�d���������n�L�[������
�m�a�n�z��`���̐��������͂���āA�e�Z���Ɍ��ʂ��\�������
�m�b�n�Z���͈͂̑I���i���]�\���j����������
 �@EX4A754Z
�@EX4A754Z
 �@EX4A751Z
�@EX4A751Z
 �@
�@
EX4A752Z�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A753Z
�������W��
���鐔�l�̘a�̊K��ƊK��̐ςƂ̔�𑽍��W���Ƃ����܂��B���̒l�����߂���́m���̓c�[���n���Z�b�g�A�b�v����уA�h�C���o�^����Ă��邱�Ƃ��K�v�ł��B
���l�t�k�s�h�m�n�l�h�`�k�� �v ���̓c�[��
�w�肳�ꂽ���l�̘a�̊K��ƁA�w�肳�ꂽ���l�̊K��̐ςƂ̔�i�����W���j��Ԃ��B
���� MULTINOMIAL(���l1, ���l2, ...)
���l1, ���l2�A... �v�Z�̑ΏۂƂȂ鐔�l���w�肷��i�ő�Q�X�܂Łj
�����W���̌v�Z�͎��̂悤�ɒ�`����Ă��܂��B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A120Z
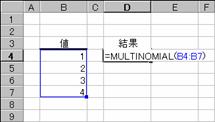
�g�p��
�m�`�n��������͂���
�m�a�n���ʂ����߂���
 �@
�@
EX4A755Z�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A756Z
���g�ݍ��킹�̐�
����X�|�[�c�̑��������̉A���邢�́A�g�ݍ��킹�������߂��������܂��B
���b�n�l�a�h�m��
���ׂĂ̍��ڂ���w�肳�ꂽ����I������Ƃ��̑g�ݍ��킹�̐���Ԃ��B�����̍��ڂ��O���[�v������Ƃ��A���Ƃ���̃O���[�v���쐬�ł��邩�ׂ�Ƃ��Ɏg�p�ł��܂��B
���� COMBIN(����, ������萔)
���� ���ڂ̐����w�肷��B
������萔 �g�ݍ��킹��1�g�Ɋ܂܂�鍀�ڂ̐����w�肷��B
����ł́A�I���������ڂ̏����ɈӖ�������̂ɑ��A�g�ݍ��킹�ł́A���ڂ̏����ɈӖ��͂���܂���B����=n�A������萔=k�Ƃ���ƁA�g�ݍ��킹�̑����́A���̐����ŕ\����܂��B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A052Z
������
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ EX4A053Z
�g�p��
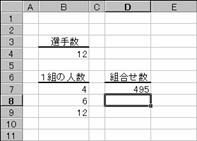
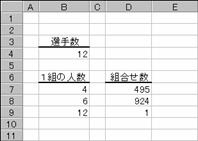
���̗�́A�P�Q�l�̑I�肩��S�l1�g�A�U�l1�g�A�P�Q�l1�g�A�̃`�[�������g�ݍ��킹�������߂Ă��܂��B
�m�`�n��������͂���
�m�a�n���ʂ����߂���
�m�b�n���֑����Z���ɐ����ʂ���
 �@
�@ �@
�@
EX4A757Z�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A758Z�@�@�@�@�@�@�@�@�@�@�@EX4A759Z
�����[�}����
���l�i�A���r�A�����j�����[�}�����ɕϊ������������܂��B���[�}�����̏����Ƃ��āA�����A�ȈՁA�̐��킩��I���������ʂ����߂邱�Ƃ��ł��܂��B
���q�n�l�`�m��
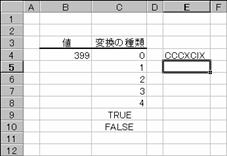
�A���r�A���������[�}������\��������ɕϊ�����B
���� ROMAN(���l, ����)
���l �ϊ����鐔�l�i�A���r�A�����j���w�肷��B
���� ���[�}�����̏����𐔒l�Ŏw�肷��B
���� ���
0/�ȗ� �����B
1 �ȗ��������`���B�g�p����Q�ƁB
2 1 ���ȗ��������`���B�g�p����Q�ƁB
3 2 ���ȗ��������`���B�g�p����Q�ƁB
4 �����B
TRUE �����B
FALSE �����B
���l�ɕ��̐��A�����3999���傫�����l���w�肷��ƁA�G���[�l#VALUE!���Ԃ���܂��B
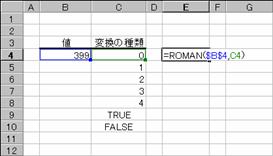
�g�p��
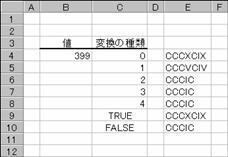
�m�`�n��������͂���
�m�a�n���ʂ����߂���
�m�b�n���֑����Z���ɐ����ʂ���
 |
 �@
�@
EX4A768Z�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A769Z
 �@EX4A770Z
�@EX4A770Z
���ׂ�����
�ׂ������́A����l�̋ߎ��v�Z���s���Ƃ��ɗ��p����l�𒊏o������ł��B�ׂ������ŋߎ��v�Z�̂ł�����ɂ��Ă͐��w���Ȃǂ��Q�l�ɂ��Ă��������B
���r�d�q�h�d�r�r�t�l�� �v ���̓c�[��
���̎��Œ�`�����ׂ�������Ԃ��B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A122Z
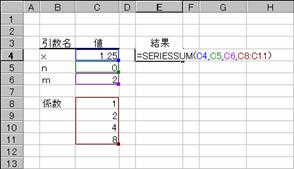
���� SERIESSUM(x, n, m, �W��)
x �ׂ������ɑ������l���w�肷��B
n x�ׂ̂���̏����l���w�肷��B
m �����̊e���ɑ���n�̑������w�肷��B
�W�� x��(n+m)��̏搔���w�肷��B
�W���Ɋ܂܂��l�̌��łׂ������̍��������肵�܂��B���Ƃ��ΌW���ɂS�̒l���܂܂�Ă���ꍇ�A�S���ׂ̂����������߂��܂��B
�g�p��
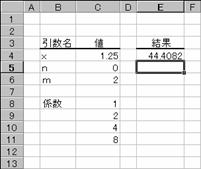
�}�̂悤�ȃf�[�^�̏ꍇ�A�S���ׂ̂����������߂��܂��B
�m�`�n��������͂���
�m�a�n���ʂ����߂���
 �@
�@
EX4A771Z�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A772Z
��������
�����������߂���ɂ́A���l�̕�������Ԃ����ƁA�̕������i�l���Δ{����j��Ԃ���������܂��B
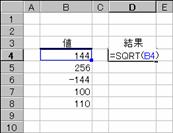
���r�p�q�s��
���̕�������Ԃ��B
���� SQRT(���l)
���l �����������߂鐔�l���w�肷��B
���l�ɕ��̐����w�肷��ƃG���[�l#NUM!���Ԃ���܂��B
�g�p��
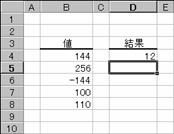
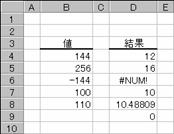
�m�`�n��������͂���
�m�a�n���ʂ����߂���
�m�b�n���֑����Z���ɐ����ʂ���
�͂O�i�[���j�Ƃ��Čv�Z����܂��i�Z���c�X�Q�l�j�B�����͌v�Z�ł��Ȃ��̂ŁA���m�t�l�I���Ԃ���Ă��܂��i�Z���c�U�Q�l�j�B
 �@
�@ �@
�@
EX4A760Z�@�@�@�@�@�@�@�@�@�@EX4A761Z�@�@�@�@�@�@�@�@�@�@EX4A762Z
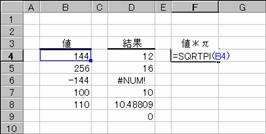
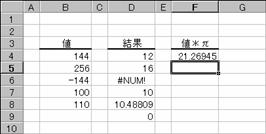
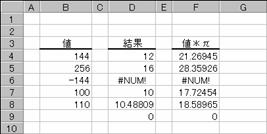
���r�p�q�s�o�h�� �v ���̓c�[��
���l���̕�������Ԃ��B
���� SQRTPI(���l)
���l �Δ{���鐔�l���w�肷��B
���l�ɕ������w�肷��ƁA�G���[�l#NUM!���Ԃ���܂��B
�g�p��
�m�`�n��������͂���
�m�a�n���ʂ����߂���
�m�b�n���֑����Z���ɐ����ʂ���
 �@
�@
EX4A763Z�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A764Z
 �@EX4A765Z
�@EX4A765Z
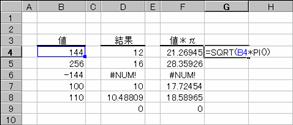
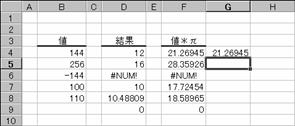
���̗�́ASQRTPI�����g��Ȃ��œ������ʂ����߂Ă��܂��B
�m�`�n��������͂���
�m�a�n���ʂ����߂���
 �@
�@
EX4A766Z�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A767Z
�������a
����l���悵���l�����v�����l�̂��Ƃ��a�Ƃ����܂��B���̊��̊��p��Ƃ��ẮA�~�n�̑��ʐς̌v�Z�Ȃǂɗ��p���܂��B
���r�t�l�r�p��
�����̂Q��̘a�i�����a�j��Ԃ��B
���� SUMSQ(���l1, ���l2, ...)
���l1, ���l2,... �����a���v�Z���鐔�l���w�肷��i�ő�R�O�܂Łj
�g�p��
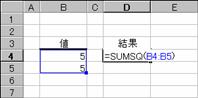
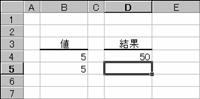
���̗�͂Q�̒l�i�T�̕����͂Q�T�j�̕����a�����߂Ă��܂��B
�m�`�n��������͂���
�m�a�n���ʂ����߂���
 �@
�@
EX4A773Z�@�@�@�@�@�@�@�@�@�@�@�@EX4A774Z
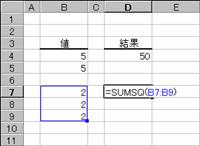
���̗�͂R�̒l�̕����a�����߂Ă��܂��B
�m�`�n��������͂���
�m�a�n���ʂ����߂���
 �@
�@
EX4A775Z�@�@�@�@�@�@�@�@�@�@�@�@EX4A776Z
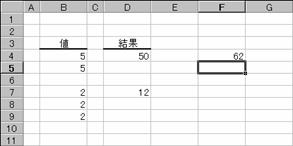
�ȏ�̗�ł́A�l�͂Q��R�ł������A�Z���͈͂Ŏw�肵�Ă���̂ň����Ƃ��Ă͂P�i�ő�R�O�̂����̂P�j�ł��B���̗�ł́A�����͂Q�ɂȂ�܂��B
�m�`�n��������͂���
�m�a�n���ʂ����߂���
 �@EX4A777Z
�@EX4A777Z
 �@EX4A778Z
�@EX4A778Z
�쐬�菇
�@���āA�ǂ����珑���n�߂�����̂ł��傤�B
 |
|||||
 |
|||||
 |
|||||
 |
|
 |