�R�|�S�@������
�@�������̓h���P�ʂ���ɂȂ��Ă�����̂�����܂��B���{�����ł̎Z�o���@�ƈ���Ă���ꍇ������A�s�K�Ȓl���Ԃ���邱�Ƃ�����̂ŁA���߂��l�����{�����Ŏg�p����l�ɓK�����Ă��邩���m���߂Ă�����ۂ̋Ɩ��Ɏg���悤�ɂ��Ă��������B�Ȃ��A�������̉��p����́u���K�C�h�v�ł�������Ă���̂ŎQ�l�ɂ��Ă��������B�Ȃ��A�����Ȃǂ̒P�ʂɁ����g���Ă���ꍇ�̓h�����Ă̊��ł��B
�����ʂ̈���
�������ɂ́A���ɋ����鋤�ʂ̈������g�p���܂��B
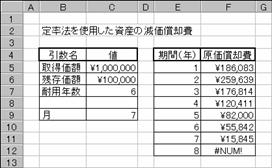
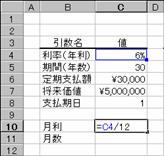
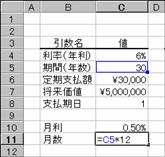
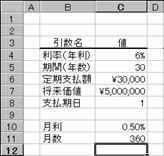
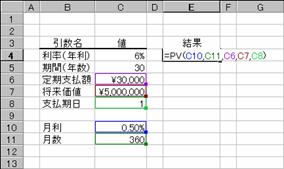
�擾���z ���Y���w���������i���w�肷��
�c�����z �ϗp�N�����I���������_�̎��Y�̉��i���w�肷��
�ϗp�N�� ���Y���g�p�ł���N���i���p�̑ΏۂƂȂ鎑�Y�̎����N���j���w�肷��
���� �������p������߂���i�N�j���w�肷��
�� ���Y���w�������N�̌������A1�`12�͈̔͂Ŏw�肷��B�ȗ���12�ɂȂ�
�� �������p���i�P���P�O�O���j���w�肷��B
�J�n�� �������p��̌v�Z�̑ΏۂƂȂ�ŏ��̊����w�肷��B�i�ϗp�N���Ɠ����P�ʂŎw��j
�I���� �������p��̌v�Z�̑ΏۂƂȂ�Ō�̊����w�肷��B�i�ϗp�N���Ɠ����P�ʂŎw��j
�p�x �@�@�N�Ԃ̗����x�����w�肷��B�P���N1��A�Q���N2��A�S���l��������
� �@�@�����̌v�Z���@�𐔒l�Ŏw�肷��B
� 1�����̓��� /1�N�̓���
0/�ȗ� 30�� /360��(NASD����)
1 ���ۂ̓��� /���ۂ̓���
2 ���ۂ̓��� /360��
3 ���ۂ̓��� /365��
4 30�� /360��(���[���b�p����)
�p�x �N�Ԃ̗����x�����w�肷��B�P���N1��A�Q���N2��A�S���l��������
�p�x�ɂP�A�Q�A�S�A�ȊO�̐��l���w�肷��ƃG���[�l#NUM!���Ԃ���܂��B���s���A�ŏ��̗������A��̓��A�p�x�A��A�ɐ����ȊO�̒l���w�肷��Ə����_�ȉ�����̂Ă��܂��B
�y���Ӂz
���@Windows �� Excel �� Macintosh �� Excel �ł́A�W���Ƃ��Ďg�p�������t�V�X�e�����قȂ�܂��B�ڍׂɂ��Ă� NOW �����Q�Ƃ��Ă��������B
���������p
�������p������߂���Ƃ��āA�藦�@�i�c�a���j�A�{���@�i�c�c�a���j�A��z�@�i�u�c�a���j�A���g�������̂��g�ݍ��܂�Ă��܂��B���ꂼ��̊��Ɏw�肷�铯�������̒P�ʂ���e�͋��ʎd�l�ɂȂ��Ă��܂��B
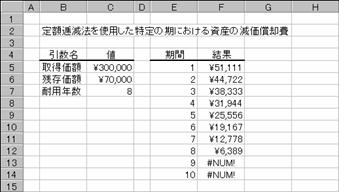
���� DB(�擾���z, �c�����z, �ϗp�N��, ����, ��)
DDB(�擾���z, �c�����z, �ϗp�N��, ����, ��)
VDB(�擾���z, �c�����z, �ϗp�N��, �J�n��, �I����, ��, �ؑւȂ�)
�m�������n �m�ݒ���e�n���ؑւȂ��ȊO�̈����͕K�����̐��Ŏw�肷��
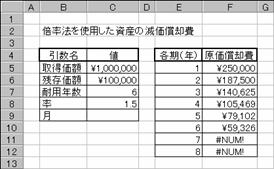
�擾���z ���Y���w���������i���w�肷��
�c�����z �ϗp�N�����I���������_�̎��Y�̉��i���w�肷��
�ϗp�N�� ���Y���g�p�ł���N���i���p�̑ΏۂƂȂ鎑�Y�̎����N���j���w�肷��
���� �������p������߂���i�N�j���w�肷��
�� ���Y���w�������N�̌������A1�`12�͈̔͂Ŏw�肷��B�ȗ���12�ɂȂ�
�� �������p���i�P���P�O�O���j���w�肷��B�ȗ���2�ƌ��Ȃ���{�������@�Ōv�Z�����
�J�n�� �������p��̌v�Z�̑ΏۂƂȂ�ŏ��̊����w�肷��B�i�ϗp�N���Ɠ����P�ʂŎw��j
�I���� �������p��̌v�Z�̑ΏۂƂȂ�Ō�̊����w�肷��B�i�ϗp�N���Ɠ����P�ʂŎw��j
�ؑւȂ� �������p��{���@�ɂ��v�Z�̌��ʂ��傫���Ȃ����Ƃ��ɁA�����I�ɒ�z�@�ɐ�ւ��邩�ǂ�����_���l�Ŏw�肷��B
TRUE ��z�@�ւ̐�ւ��͍s��Ȃ�
FALSE ��z�@�ւ̐�ւ����s�Ȃ��i�ȗ����j
���c�a���@�藦�@(Fixed-declining Balance Method)
�@�藦�@���g�p��������̊��ɂ����鎑�Y�̌������p��͂c�a���ŋ��߂܂��B�藦�@�́A�Œ藘���Ō������p��v�Z����܂��B�v�Z�͎��̐����Ɠ����ɂȂ�܂��B
�ŏ��̊��ɑ��錸�����p��͎��̐����ŕ\����܂��B
�擾���z * ���p�� * �� / 12
���Ԋ��ɑ��錸�����p��͎��̐����ŕ\����܂��B
(�擾���z - �O���܂ł̏��p��v�z) * ���p��
�Ō�̊��ɑ��錸�����p��͎��̐����ŕ\����܂��B
((�擾���z - �O���܂ł̏��p��v�z) * ���p�� * (12 - ��)) / 12
������
���p�� = 1 - ((�c�����z / �擾���z) ^ (1 / �ϗp�N��))
�g�p��
�p�\�R����100���~�ōw�����܂����B���̃p�\�R���̎c�����z��10���~�A�ϗp�N����6�N���Ƃ��܂��B���N�x�̌�����7���ł���ꍇ�A�e��(�N)�̌������p��͎��̂悤�ɋ��߂��܂��B�ŏ��̊��i�P�N�ځj�ƍŌ�̊��i�V�N�ځj�̋��z���Ⴂ�͎̂擾���i�V���j�Ō�����v�Z�ɂȂ��Ă��邩��ł��B�W�N�ڂ̌��ʂɁ��m�t�l�I���\�������̂́A���p��Ȃ��i�[���j��\���܂��B�v�Z���ʂ͐����Ɏl�̌ܓ�����܂��B
 �@EX4A144Z
�@EX4A144Z
���͂��鐔��
F5 : =DB($C$5,$C$6,$C$7,E5,$C$9)
F6 : =DB($C$5,$C$6,$C$7,E6,$C$9)
F7 : =DB($C$5,$C$6,$C$7,E7,$C$9)
F8 : =DB($C$5,$C$6,$C$7,E8,$C$9)
F9 : =DB($C$5,$C$6,$C$7,E9,$C$9)
F10: =DB($C$5,$C$6,$C$7,E10,$C$9)
F11: =DB($C$5,$C$6,$C$7,E11,$C$9)
���c�c�a���@�{���@(Double-declining Balance Method)
�w�肷�鏞�p���Ō������p��v�Z����܂��B�������p��́A�ŏ��̊����ł������A���̌�̊��ł͋}���Ɍ������Ă����܂��B�e���̌������p��͎��̐����ŕ\�Ɠ����ɂȂ�܂��B
�擾���z - �c�����z (�O���܂ł̏��p��v�z) * �� / �ϗp�N��
�g�p��
��̗���c�c�a���ŋ��߂�Ǝ��̂悤�ɂȌ������p��ɂȂ�܂��B�}�`�͔N�P�ʂŋ��߂��ꍇ�A�}�a�͓��P�ʂŌ������p������߂Ă��܂��B�����m�ϗp�N���n������Ŏw�肵���ꍇ�A�����m���ԁn�̎w��������ōs�����Ƃ��K�v�ł��B�}�`�C�a�Ƃ��ɓ��͂��鐔���͓����ŁA���ږ��ƈ����̒l�����������ւ��Ă��܂��B
�}�`�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�}�a
 �@
�@
EX4A145Z�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A146Z
F5 : =DDB($C$5,$C$6,$C$7,E5,$C$8)
F6 : =DDB($C$5,$C$6,$C$7,E6,$C$8)
F7 : =DDB($C$5,$C$6,$C$7,E7,$C$8)
F8 : =DDB($C$5,$C$6,$C$7,E8,$C$8)
F9 : =DDB($C$5,$C$6,$C$7,E9,$C$8)
F10: =DDB($C$5,$C$6,$C$7,E10,$C$8)
F11: =DDB($C$5,$C$6,$C$7,E11,$C$8)
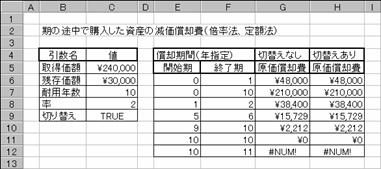
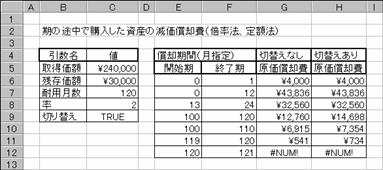
���u�c�a���@�{�������@(Variable Declining Balance)
�@�{�������@�܂��͎w�肳�ꂽ���@���g�p���āA�w�肳�ꂽ���Ԃɂ����鎑�Y�̌������p���Ԃ��B
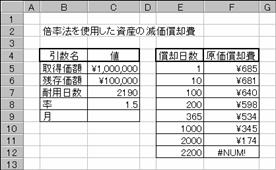
���� VDB(�擾���z, �c�����z, �ϗp�N��, �J�n��, �I����, ��, �ؑւȂ�)
�g�p��
�ϗp�N���P�O�N�̃��[�U�[�v�����^���Q�S���~�ōw�����܂����B���̃v�����^�̎c�����i���R���~�ł���Ƃ��A������Ԃ̌������p��͎��̂悤�ɂȂ�܂��B�}�`�͔N�P�ʂŋ��߂��ꍇ�A�}�a�͌��P�ʂŌ������p������߂Ă��܂��B�����m�ϗp�N���n�������Ŏw�肵���ꍇ�A�����m���ԁn�̎w��������ōs�����Ƃ��K�v�ł��B�}�`�C�a�Ƃ��ɓ��͂��鐔���͓����ŁA���ږ��ƈ����̒l�����������ւ��Ă��܂��B
�}�`
 �@EX4A148Z
�@EX4A148Z
�}�a
 �@EX4A147Z
�@EX4A147Z
C9 :=TRUE()
G6 :=VDB($C$5,$C$6,$C$7,E6,F6,$C$8,$C$9)
G7 :=VDB($C$5,$C$6,$C$7,E7,F7,$C$8,$C$9)
G8 :=VDB($C$5,$C$6,$C$7,E8,F8,$C$8,$C$9)
G9 :=VDB($C$5,$C$6,$C$7,E9,F9,$C$8,$C$9)
G10:=VDB($C$5,$C$6,$C$7,E10,F10,$C$8,$C$9)
G11:=VDB($C$5,$C$6,$C$7,E11,F11,$C$8,$C$9)
G12:=VDB($C$5,$C$6,$C$7,E12,F12,$C$8,$C$9)
H6 :=VDB($C$5,$C$6,$C$7,E6,F6,$C$8,FALSE())
H7 :=VDB($C$5,$C$6,$C$7,E7,F7,$C$8,"FALSE")
H8 :=VDB($C$5,$C$6,$C$7,E8,F8,$C$8,FALSE())
H9 :=VDB($C$5,$C$6,$C$7,E9,F9,$C$8,FALSE())
H10:=VDB($C$5,$C$6,$C$7,E10,F10,$C$8,"FALSE")
H11:=VDB($C$5,$C$6,$C$7,E11,F11,$C$8,FALSE())
H12:=VDB($C$5,$C$6,$C$7,E12,F12,$C$8,FALSE())
�����m�ؑւȂ��n�́A���p�̕�����A���邢�͘_�����Ŏw�肵�܂��B
��@������Ŏw�肷��ꍇ
VDB(240000,30000,120,100,120,2,"TRUE") = \12,760
�@�@�_�����Ŏw�肷��ꍇ
VDB(240000,30000,120,100,120,2,TRUE()) = \12,760
���r�k�m��
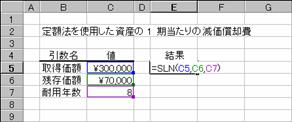
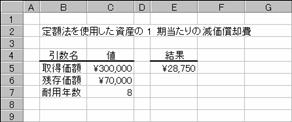
��z�@�i�r���������������|���������@�l�����������j���g�p���āA���Y�̂P��������̌������p���Ԃ��B
���� SLN(�擾���z, �c�����z, �ϗp�N��)
�擾���z ���Y�̍w�����i���w�肷��
�c�����z �ϗp�N�����I���������_�̉��i���w�肷��
�ϗp�N�� ���Y���g�p�ł���N���i���p�̑ΏۂƂȂ鎑�Y�̎����N���j���w�肷��B
�g�p��
�ϗp�N���W�N�̃��[�U�[�v�����^���R�O���~�ōw�����܂����B���̃v�����^�̎c�����i���V���~�ł���Ƃ��A�P��������̌������p��͎��̂悤�ɂȂ�܂��B
�m�`�n�Z���d�T�ɁA�������Z���Q�ƂŎw�肵���r�k�m������͂���
�m�a�n����
�}�`�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�}�a
 �@
�@
EX4A269Z�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A270Z
���r�x�c��
��z�����@�i�r�����|�����|�x�������f���@�c�����������@�l�����������j���g�p���āA�w����Ԃ̌������p���Ԃ��B
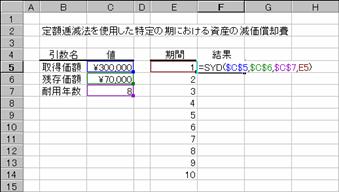
���� SYD(�擾���z, �c�����z, �ϗp�N��, ����)
�擾���z ���Y�̍w�����i���w�肷��
�c�����z �ϗp�N�����I���������_�̉��i���w�肷��
�ϗp�N�� ���Y���g�p�ł���N���i���p�̑ΏۂƂȂ鎑�Y�̎����N���j���w�肷��B
���� �������p������߂���Ԃ��w�肷��i�ϗp�N���Ɠ����P�ʂŎw�肷��j
�g�p��
�ϗp�N���W�N�̃��[�U�[�v�����^���R�O���~�ōw�����܂����B���̃v�����^�̎c�����i���V���~�ł���Ƃ��A�e���ԓ�����̌������p��͐}�a�̂悤�ɁA���ԂP�i�P�N�ځj�́��T�P�C�P�P�P�A���ԂQ�i�Q�N�ځj�́��S�S�C�V�Q�Q�Ȃ�܂��B�X�N�ڂƂP�O�N�ڂ̃G���[���m�t�l�I�͏��p��O�~��\���܂��B
�@�Z���e�T�Ɉ����m�擾���z, �c�����z, �ϗp�N���n���Z���Ԓn�A�����m���ԁn�𑊑Z���Ԓn�Ŏw�肵�āA�Z���e�U�`�e�P�S�ɕ��ʂ��܂��B���ʌ�̊e�����͈ȉ��̂悤�ɂȂ�܂��B
�Z���e�T�@���r�x�c�i���b���T�C���b���U�C���b���V�C�d�T�j
�Z���e�U�@���r�x�c�i���b���T�C���b���U�C���b���V�C�d�U�j
�Z���e�V�@���r�x�c�i���b���T�C���b���U�C���b���V�C�d�V�j
�Z���e�W�@���r�x�c�i���b���T�C���b���U�C���b���V�C�d�W�j
�Z���e�X�@���r�x�c�i���b���T�C���b���U�C���b���V�C�d�X�j
�Z���e�P�O���r�x�c�i���b���T�C���b���U�C���b���V�C�d�P�O�j
�Z���e�P�P���r�x�c�i���b���T�C���b���U�C���b���V�C�d�P�P�j
�Z���e�P�Q���r�x�c�i���b���T�C���b���U�C���b���V�C�d�P�Q�j
�Z���e�P�R���r�x�c�i���b���T�C���b���U�C���b���V�C�d�P�R�j
�Z���e�P�S���r�x�c�i���b���T�C���b���U�C���b���V�C�d�P�S�j
�m�`�n�Z���e�T�ɐ�������͂���
���Z���e�T�����֑����Z���e�U�`�e�P�S�ɕ��ʂ���
�m�a�n����
�}�`
 �@EX4A271Z
�@EX4A271Z
�}�a
 �@EX4A272Z
�@EX4A272Z
�y�܂Ƃ߁z
DB �藦�@���g�p���āA����̊��ɂ����鎑�Y�̌������p���Ԃ��B
DDB �{���@���g�p���āA����̊��ɂ����鎑�Y�̌������p���Ԃ��B
VDB �{���@���g�p���āA���̓r���ōw���������Y�̌������p���Ԃ��B
SLN ��z�@���g�p���āA���Y��1��������̌������p���Ԃ��B
SYD ��z�����@���g�p���āA����̊��ɂ����鎑�Y�̌������p���Ԃ��B
���̂Q�̊��̓t�����X���̉�v�V�X�e���p�ł��B
�@AMORDEGRC �e��v���ɂ����錸�����p���Ԃ��B
�@AMORLINC �e��v���ɂ����錸�����p���Ԃ��B
��AMORDEGRC��
�e��v���ɂ����錸�����p���Ԃ��B���̊���AMORLINC���Ɏ��Ă��܂����A���Y�̑ϗp�N���ɉ����Ĉ��̌������p�W�����v�Z�ɓK�p�����_���قȂ�܂��B
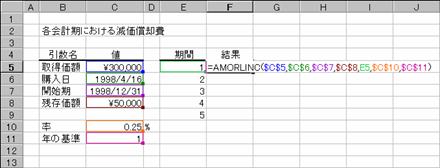
���� AMORDEGRC(�擾���z, �w����, �J�n��, �c�����z, ��, ��, �N�̊)
�擾���z ���Y���w���������_�ł̉��i���w�肷��B
�w���� ���Y���w���������t���w�肷��B
�J�n�� �ŏ��̉�v�����I��������t���w�肷��B
�c�����z �ϗp�N�����I���������_�ł̎��Y�̉��i���w�肷��B
�� ���߂��v���i��v�N�x�j���w�肷��B
�� �������p�����w�肷��B
�N�̊ 1�N�������Ƃ��Čv�Z���邩�𐔒l�Ŏw�肷��B
�������p�W���́A���̂悤�ɒ�`����Ă��܂��B
���Y�̑ϗp�N�� �������p�W��
3 �` 4 �N 1.5
5 �` 6 �N 2
6 �N�ȏ� 2.5
�������p���́A�Ōォ��P�O�̊��łT�O���܂ŏ㏸���A�Ō�̉�v���łP�O�O���܂ŏ㏸���܂��B���Y�̑ϗp�N�����O�`�P�N�A�P�`�Q�N�A�Q�`�R�N�A�܂��͂S�`�T�N�ł���ꍇ�A�G���[�l���m�t�l�I���Ԃ���܂��B
�g�p��
�V�����R���s���[�^���S�W���~�łP�X�X�W�N�S���P�U���ɍw�����܂����B���̃R���s���[�^�̎c�����z�͂T���~�A�ϗp�N�����W�N�Ō������p���͂Q�T���i�W���Q�D�T�j���Ƃ���A�e��v���i���Ԃ�N���Ŏw��j�͐}�a�̂悤�ɋ��߂��܂��B���ӁA���̒l�͂P�X�O�O�N���t�V�X�e��(Windows��Excel�̕W��)�̏ꍇ�ł��B
�m�`�n�Z���e�T�ɐ�������͂��āA���ɑ����Z���e�U�`�e�X�ɕ��ʂ���
�Z���e�T�@���`�l�n�q�c�d�f�q�b�i���b���T�C���b���U�C���b���V�C���b���W�C�d�T�C
�@�@���b���P�O�C���b���P�P�j
�m�a�n����
�m�`�n
 �@EX4A273Z
�@EX4A273Z
�m�a�n
 �@EX4A274Z
�@EX4A274Z
���`�l�n�q�k�h�m�b��
�e��v���ɂ����錸�����p���Ԃ��B���Y����v���̓r���ōw�������ꍇ�A������v�Z�ɂ�錸�����p��v�コ��܂��B
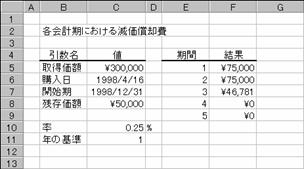
���� AMORLINC(�擾���z, �w����, �J�n��, �c�����z, ��, ��, �N�̊)
�擾���z ���Y���w���������_�ł̉��i���w�肷��B
�w���� ���Y���w���������t���w�肷��B
�J�n�� �ŏ��̉�v�����I��������t���w�肷��B
�c�����z �ϗp�N�����I���������_�ł̎��Y�̉��i���w�肷��B
�� ��v�� (��v�N�x) ���w�肷��B
�� �������p�����w�肷��B
�N�̊ 1 �N�������Ƃ��Čv�Z���邩�𐔒l�Ŏw�肷��B
�g�p��
�V�����R���s���[�^���S�W���~�łP�X�X�W�N�S���P�U���ɍw�����܂����B���̃R���s���[�^�̎c�����z�͂T���~�A�ϗp�N�����W�N�Ō������p���͂Q�T���i�W���Q�D�T�j���Ƃ���A�e��v���i���Ԃ�N���Ŏw��j�͐}�a�̂悤�ɋ��߂��܂��B���ӁA���̒l�͂P�X�O�O�N���t�V�X�e��(Windows��Excel�̕W��)�̏ꍇ�ł��B
�m�`�n�Z���e�T�ɐ�������͂��āA���ɑ����Z���e�U�`�e�X�ɕ��ʂ���
�Z���e�T�@���`�l�n�q�k�h�m�b�i���b���T�C���b���U�C���b���V�C���b���W�C�d�T�C
�@�@���b���P�O�C���b���P�P�j
�m�a�n����
�}�`
 �@EX4A275Z
�@EX4A275Z
�}�a
 �@EX4A276Z
�@EX4A276Z
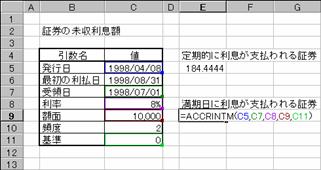
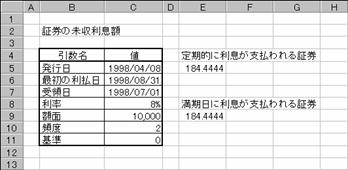
���،��̖��������z �v ���̓c�[��
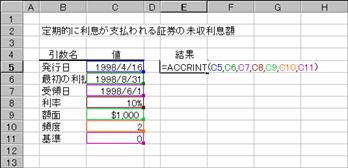
����I�ɗ������x������،��̖��������z�����߂�ACCRINT���ƁA�������ɗ������x������،��̖��������z�����߂�ACCRINTM��������܂��B���ꂼ��̏������͈ȉ��̒ʂ�ł��B
�����m����I�ɗ������x������،��n
ACCRINT(���s��, �ŏ��̗�����, ��̓�, ����, �z��, �p�x, �)
�����m�������ɗ������x������،��n
ACCRINTM(���s��, ��̓�, ����, �z��, �)
���s�� �،��̔��s�����w�肷��B
�ŏ��̗����� �،��̗������ŏ��Ɏx��������t���w�肷��B
��̓� �،��̎�̓��i�،����w���������t�j���w�肷��B
���� �،��̔N�����w�肷��B
�z�� �،��̊z�ʉ��i���w�肷��B�z�ʂ��ȗ�����ƁA$1,000���w�肵���ƌ��Ȃ���܂��B
�p�x �N�Ԃ̗����x�����w�肷��B�P���N1��A�Q���N2��A�S���l��������
� �����̌v�Z���@�𐔒l�Ŏw�肷��B�i�w��l�͂o�Q�Q�Q�Q�Ɓj�B
���������O�܂��͊z�ʁ����O�ł���ꍇ�A���s��������̓��ł���ꍇ�A�G���[�l#NUM!���Ԃ���܂��BACCRINT���́A���̐����ŕ\����܂��B
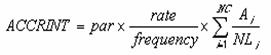 �@EX4A277Z
�@EX4A277Z
�������@�@���@�z��
���������@���@����
�������������������@���@�p�x
�`���@���@���������[�Ȋ��Ɋ܂܂�邉�Ԗڂ̏����D���̓���
�m�b�@���@���������[�Ȋ��ƈ�v���鏀���D���̐��i�����_�ȉ��͐����ɐ�グ���܂��j
�m�k���@���@���������[�Ȋ��Ɋ܂܂�邉�Ԗڂ̏����D���̓����i�W���̒l�j
ACCRINTM���́A���̐����ŕ\����܂��B
![]() �@EX4A280Z
�@EX4A280Z
�������@�@���@�z��
���������@���@����
�`�@ �@���@�����v�Z���Ԃ̓���
�c�@ �@���@�����v�Z�̊�ƂȂ�P�N�̓���
�g�p��m����I�ɗ������x������،��n
���̂s�a�i�č������Ȕ��s�̒������j�̏ꍇ�A���������z�͐}�a�̂悤�ɋ��߂��܂��B
���s��: �P�X�X�W�N�S���P�U��
��̓�: �P�X�X�W�N�U���P��
�ŏ��̗����x����: �P�X�X�W�N�W���R�P��
����: �P�O�D�O��
�z�ʉ��i: ���P�C�O�O�O
�����x����: �N 2 ��
�: �O�i30 ��/360 ���j
���̗�̈��������ɒ��ړ��͂���ꍇ�͈ȉ��̂悤�ɓ��t�������^�����^�����`���œ��͂��܂��B
=ACCRINT("4/16/98","8/31/98","6/1/98",0.1,1000,2,0)
�m�`�n�Z���d�T�ɐ�������͂���
���`�b�b�q�h�m�s�i�b�T�C�b�U�C�b�V�C�b�W�C�b�X�C�b�P�O�C�b�P�P�j
�m�a�n����
�}�`�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�}�a
 �@
�@
EX4A278Z�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A279Z
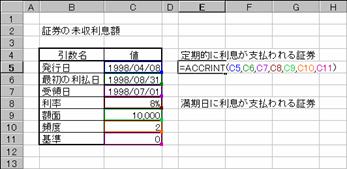
�g�p��m�������ɗ������x������،��n
���̂s�a�i�č������Ȕ��s�̒������j�̏ꍇ�A���������z�͐}�d�i�Z���d�T�j�̂悤�ɋ��߂��܂��B���������i�����j���g�p����ACCRINTM����ACCRINT���̌��ʂ��ׂĂ��܂��B
���s��: 1993 �N 4 �� 1 ��
��̓�: 1993 �N 6 �� 15 ��
����: 10.0%
�z�ʉ��i: $1000
�: ���ۂ̓���/365 ��
���̗�̈��������ɒ��ړ��͂���ꍇ�͈ȉ��̂悤�ɓ��t�������^�����^�����`���œ��͂��܂��B
��ACCRINTM("4/1/93","6/15/93",0.1,1000,3)
�m�`�n�Z���d�X��ACCRINT������͂���
�m�a�n�Z���d�T��ACCRINTM������͂���
�m�b�n����
 �@EX4A281Z
�@EX4A281Z
 �@EX4A282Z
�@EX4A282Z
�}�d
 �@EX4A283Z
�@EX4A283Z
�y���Ӂz
���@Windows��Excel��Macintosh��Excel�ł́A�W���Ƃ��Ďg�p�������t�V�X�e�����قȂ�܂��B�ڍׂɂ��Ă�NOW�����Q�Ƃ��Ă��������B
�� ���ɓ��t����͂���ꍇ�A�����^�����^�����`���Łh�h�ň͂�œ��͂��邱�Ƃ��K�v�ł��B
�y�܂Ƃ߁z
ACCRINT ����I�ɗ������x������،��̖��������z��Ԃ��B
ACCRINTM �������ɗ������x������،��̖��������z��Ԃ��B
���������Ɠ��� �v ���̓c�[��
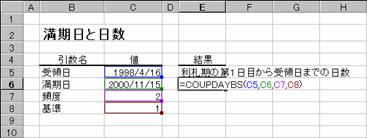
�،��̖������Ǝ�̓��◘�����܂ł̓��������߂���ɂ́A���̂��̂�����܂��B
COUPDAYBS���́A���D���̑� 1 ���ڂ����̓��܂ł̓�����Ԃ��B
COUPDAYS���͎�̓����܂ޗ��D���̓�����Ԃ��B
COUPDAYSNC���́A��̓����玟�̗����x�����܂ł̓�����Ԃ��B
COUPNCD���́A��̓��̒���̗����x�����𐔒l�ŕԂ��B
COUPNUM���́A��̓��Ɩ������̊Ԃɗ������x�������Ԃ��B�[���͎l�̌ܓ�����܂��B
COUPPCD���́A��̓��̒��O�̗����x������Ԃ��B
���� COUPDAYBS(��̓�, ������, �p�x, �)
COUPDAYS(��̓�, ������, �p�x, �)
COUPDAYSNC(��̓�, ������, �p�x, �)
COUPNCD(��̓�, ������, �p�x, �)
COUPNUM(��̓�, ������, �p�x, �)
COUPPCD(��̓�, ������, �p�x, �)
��̓� �،��̎�̓��i�،����w���������s���j���w�肷��B
������ �،��̖������i�،��̎x�������j���w�肷��B
�p�x �N�Ԃ̗����x�����w�肷��B�P���N1��A�Q���N2��A�S���l��������
� �����̌v�Z���@�𐔒l�Ŏw�肷��B�i�w��l�͂o�Q�Q�Q�Q�Ɓj�B
�������͏،��̎x�������ł��B���Ƃ��A1998�N1��1���ɔ��s���ꂽ30�N�̍����A���s����6������ɍw������ƁA���̍��͔��s����1998�N1��1���A��̓���1998�N7��1���ɂȂ�A�������́A���s����1998�N1��1������30�N���2028�N1��1���ɂȂ�܂��B
�g�p��
���̍�������܂��B���������i�����j�Ŋe���̎g�p������Ɏ����܂��BCOUPNCD����COUPPCD���͌��ʂ���t�̃V���A���l�ŕԂ��̂ŁA�Z���̕\���`������t�ɐݒ肵�ē��t�ŕ\������悤�ɂ��܂��B
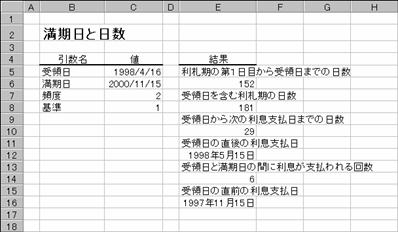
��̓�: 1998�N4��16��
������: 2000�N11��15��
�����x����: �N 2 ��
�: �P�i���ۂ̓���/���ۂ̓����j
�e�����̌��ʂ͐}�Q���������������B
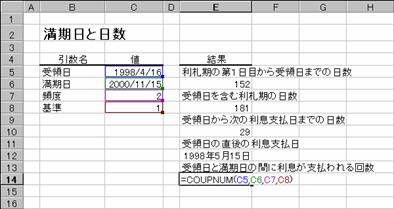
���b�n�t�o�c�`�x�a�r��
�m�`�n�Z���d�U�ɐ�������͂���
 �@EX4A284Z
�@EX4A284Z
���b�n�t�o�c�`�x�r��
�m�a�n�Z���d�W�ɐ�������͂���
 �@EX4A285Z
�@EX4A285Z
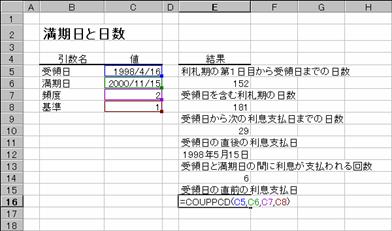
���b�n�t�o�c�`�x�r�m�b��
�m�b�n�Z���d�P�O�ɐ�������͂���
 �@EX4A286Z
�@EX4A286Z
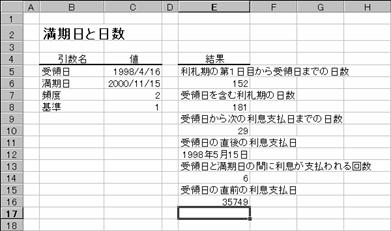
���b�n�t�o�m�b�c��
�m�c�n�Z���d�P�Q�ɐ�������͂���
�m�d�n���ʂ����t�̃V���A���l�ŋ��߂���
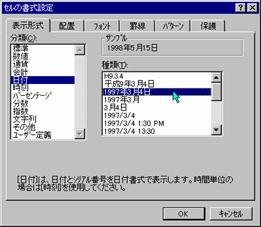
�m�e�n���Z���d�P�Q�̕\���`������t�ɐݒ肷��i�����ł́u1997�N3��4���v�`����I���j
�m�f�n���ʂ����t�ŕ\�������
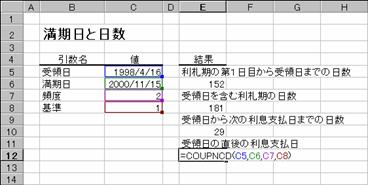 �@EX4A289Z
�@EX4A289Z
 �@EX4A287Z
�@EX4A287Z
 �@EX4A288Z
�@EX4A288Z
 �@EX4A289Z
�@EX4A289Z
���b�n�t�o�m�t�l��
�m�g�n�Z���d�P�S�ɐ�������͂���
 �@EX4A290Z
�@EX4A290Z
���b�n�t�o�o�b�c��
�m�h�n�Z���d�P�U�ɐ�������͂���
�m�i�n���ʂ����t�̃V���A���l�ŋ��߂���
���Z���d�P�U�̕\���`������t�ɐݒ肷��i�����ł́u1997�N3��4���v�`����I���j
�m�j�n���ʂ����t�ŕ\�������
 �@EX4A291Z
�@EX4A291Z
 �@EX4A292Z
�@EX4A292Z
 �@EX4A293Z
�@EX4A293Z
�y�܂Ƃ߁z
COUPDAYBS ���D���̑�1���ڂ����̓��܂ł̓�����Ԃ��B
COUPDAYS ��̓����܂ޗ��D���̓�����Ԃ��B
COUPDAYSNC ��̓����玟�̗����x�����܂ł̓�����Ԃ��B
COUPNCD ��̓��̒���̗����x������Ԃ��B
COUPNUM ��̓��Ɩ������̊Ԃɗ������x�������Ԃ��B
COUPPCD ��̓��̒��O�̗����x������Ԃ��B
���ݕt�� �v ���̓c�[��
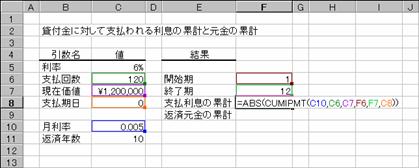
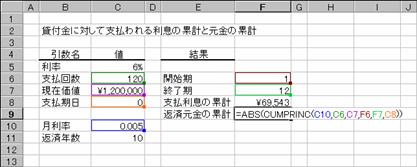
�����ʼn��������́A���[���ԍς̗v���z���v�Z���܂��BCUMIPMT���͗����̗v�ACUMPRINC���͌����̗v��Ԃ��܂��B
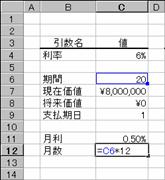
���� CUMIPMT(����, �x����, ���݉��l, �J�n��, �I����, �x������)
���� CUMPRINC(����, �x����, ���݉��l, �J�n��, �I����, �x������)
���� �ݕt�������w�肷��
�x���� �x���̍��v���w�肷��
���݉��l �ݕt�z
�J�n�� �v�Z����ŏ��̊����w�肷��
�I���� �v�Z����Ō�̊����w�肷��
�x������ �x�����̎������w�肷��
�x������ �x�������s���鎞��
0 �e���̊���i�ȗ����j
1 �e���̊���
�����m�����n�Ɓm�x���n���P�ʂŎw�肷�邱�Ƃ��K�v�ł��B���Ƃ��A�x���������P�ʂōs���ꍇ�́A�N�����P�Q�Ŋ����������Ŏw�肵�܂��B
�g�p��
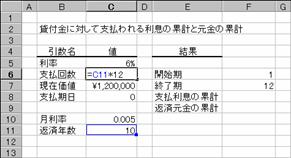
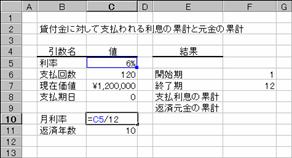
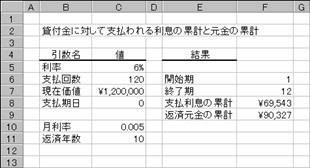
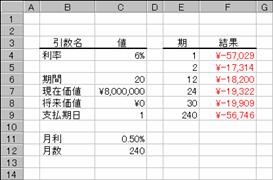
�R���s���[�^�����邽�߂ɁA�P�Q�O���~�̃��[�����ȉ��̂悤�ɂ��݂܂����B������Ԃ̕ԍϊz�͐}�a�̂悤�ɋ��߂��܂��B
�N��: 6.00%
�ԍϊ���: 10�N
���݉��l: \1,200,000
�Ԃ����l�͕����ɂȂ�̂ŁA�`�a�r���Ő����ɕϊ����Č��ʂ���₷�����Ă��܂��B�܂��A�\���`�������z�ɐݒ肵�Ă��܂��B
�������ƕԍω�
�e�f�[�^��}�`�̂悤�ɓ��͂��܂��B�ԍς��������ɂ���ꍇ�A�N�����P�Q�Ŋ������l�Ŏw�肷��̂ŃZ���b�P�O�Ō����������߂Ă��܂��B�x�����������Ŏw�肷�邱�ƂɂȂ�A�ԍϔN�����猎�������߂鐔�����Z���b�U�i�x�����j�ɓ��͂��Ă��܂��B���̈����͐��l����͂��Ă��܂��B
�m�`�n�Z���b�U�ɂ͎x������ԍϔN������v�Z���鐔�������
�m�a�n�Z���b�P�O�ɂ͗������猎�������v�Z���鐔�������
 |
 �@
�@
EX4A297Z�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A298Z
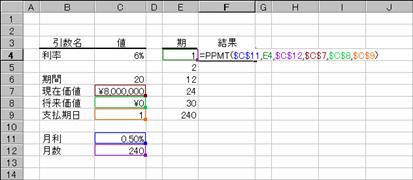
���v�Z��
�����ƌ����̗v�����߂�����`�a�r���Ƒg�ݍ��킹�ē��͂��Ă��܂��B�J�n���ɂP�A�I�����ɂP�Q����͂��āA�ŏ��̂P�N�Ԃ̌��ʂ����߂Ă��܂��B�Q�N�ڂ̗v�����߂�Ƃ��́A�J�n���ɂP�R�A�I�����ɂQ�S����͂��܂��B�}�b�ł̓Z���e�W�Ƃe�X�̕\���`�������z�ɐݒ肵�Ă��܂��B�P�O�N�̕ԍςɂ��Ă���̂ŁA�J�n���ɂP�A�I�����ɂP�Q�O���w�肷��ƕԍϑ��z�����߂��܂��B
�m�`�n�Z���e�W�ɗ����̗v�����߂鐔�������
�m�a�n�Z���e�X�ɕԍό����̗v�����߂鐔�������
 �@EX4A299Z
�@EX4A299Z
 �@EX4A300Z
�@EX4A300Z
�}�b
 �@EX4A301Z
�@EX4A301Z
�y�܂Ƃ߁z
CUMIPMT �w�肳�ꂽ���ԂɁA�ݕt���ɑ��Ďx�����闘���̗v��Ԃ��B
CUMPRINC �w�肳�ꂽ���ԂɁA�ݕt���ɑ��Ďx�����錳���̗v��Ԃ��B
�������� �v ���̓c�[��
�����ɊW������ɂ͎��̂��̂�����܂��BDISC���F�،��ɑ��銄������Ԃ��BYIELDDISC���F�����̔N������Ԃ��BPRICEDISC���F��̓��ɗ������x������،��ɑ��āA�z��$100������̉��i��Ԃ��B
���� DISC(��̓�, ������, ���݉��l, ���҉��l, �)
YIELDDISC(��̓�, ������, ���݉��l, ���҉��l, �)
PRICEDISC(��̓�, ������, ������, ���҉��l, �)
��̓� �،��̎�̓��i�،����w���������t�j���w�肷��B
������ �،��̖������i�،��̎x�������j���w�肷��B
���݉��l �z�� $100 �ɑ���،��̉��i���w�肷��B
���҉��l �z�� $100 �ɑ���،��̏��Ҋz���w�肷��B
� �����̌v�Z���@�𐔒l�Ŏw�肷��i�w��l�͂o�Q�Q�Q�Q�Ɓj�B
������ �،��̊��������w�肷��B
�g�p��
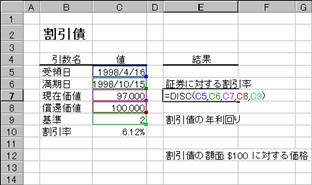
���̊�����������܂��B���̃f�[�^�����Ɋe���̌��ʂ����߂�ƈȉ��̂悤�ɂȂ�܂��B
��̓�: 1998�N4��16��
������: 1998�N10��15��
���݉��l: $97.000
���҉��l: $100
�: �Q�i���ۂ̓���/360 ���j
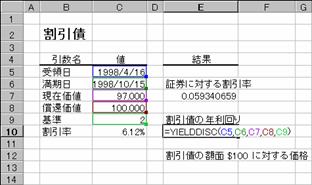
��DISC���i�،��ɑ��銄�����j
�m�`�n�Z���d�V�ɐ�������͂���
�m�a�n���ʂ͂P���P�O�O���Ƃ����l�ŕ\������܂�
 �@EX4A302Z
�@EX4A302Z
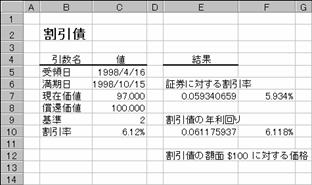
��YIELDDISC���i�����̔N�����j
�m�b�n�Z���d�P�O�ɐ�������͂���
�m�c�n���ʂ͂P���P�O�O���Ƃ����l�ŕ\������܂�
�}�d��DISC����YIELDDISC���ŋ��߂��l�����₷�����邽�߂ɁA�Z���e�V�Ƃe�P�O�ɃZ���Q�Ǝ�����͂��āA�\���`�������i�c�[���o�[�́m���n�{�^�����N���b�N����j�ɐݒ肵�ď����_�ȉ��̕\����K�ɕύX���܂��B
�m�d�n�Z���e�V�Ɂ��d�V�A�Z���e�P�O�Ɂ��d�P�O�����
 �@EX4A303Z
�@EX4A303Z
 �@EX4A304Z
�@EX4A304Z
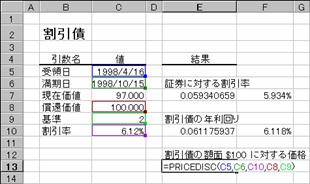
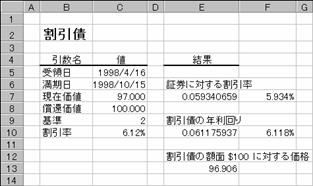
��PRICEDISC���i��̓��ɗ������x������،��̉��i�j
YIELDDISC���ŋ��߂��N���Ŋ������̉��i���t�Z����Ɛ}�e�̂悤�ɋ��߂��܂��B
�m�e�n�Z���d�P�R�ɐ�������͂���
�m�f�n���ʂ����߂���
�t�Z�̌��ʁA���݉��l�Ƒ����̍���������̂́A�����̏����_�ȉ��������܂Ŏg�����ɂ��덷�ł��B
 �@EX4A305Z
�@EX4A305Z
 �@EX4A306Z
�@EX4A306Z
�y�܂Ƃ߁z
DISC �،��ɑ��銄������Ԃ��B
YIELDDISC �����̔N������Ԃ��B
PRICEDISC �����̊z�� $100 �ɑ��鉿�i��Ԃ��B
���}�R�[���[�W�� �v ���̓c�[��
�����̕ύX�ɑ�������i�̔����̎w�W�Ƃ��Ďg�p����l�̂��Ƃ��}�R�[���[�W���Ƃ����A�L���b�V���t���[�̌��݉��l�̉��d���ςƂ��Ē�`����܂��B�}�R�[���[�W�������߂���ɂ͎��̂��̂�����܂��B
��DURATION�� �F����I�ɗ��q���x������،��̔N�Ԃ̃}�R�[���[�W����Ԃ��B
��MDURATION�� �F�z�ʉ��i��$100�Ɖ��肵�āA�،��ɑ���C���}�R�[���[�W����Ԃ��B
���� MDURATION(��̓�, ������, ���D, �����, �p�x, �)
DURATION(��̓�, ������, ���D, �����, �p�x, �)
��̓� �،��̎�̓��i�،����w���������t�j���w�肷��B
������ �،��̖������i�،��̎x�������j���w�肷��B
���D �،��̔N�����w�肷��B
����� �،��̔N�Ԕz�����w�肷��B
�p�x �N�Ԃ̗����x�����w�肷��B�P���N1��A�Q���N2��A�S���l��������
� �����̌v�Z���@�𐔒l�Ŏw�肷��i�w��l�͂o�Q�Q�Q�Q�Ɓj�B
�������̒��ӎ����͂o�Q�Q�Q�Q��
�g�p��
���̏،�������܂��B���̏،��̔N�Ԃ̃}�R�[���[�W���ƁA�z�ʉ��i�����P�O�O�Ɖ��肵���ꍇ�̏C���}�R�[���[�W���͐}�`�C�a�̂悤�ɋ��߂��܂��B
��̓�: 1990 �N 1 �� 1 ��
������: 1998 �N 1 �� 1 ��
���N�P�ʂ̗��D: 8%
�����: 9.0%
�����x����: �N 2 ��
�: �P�i���ۂ̓���/���ۂ̓����j
�}�`
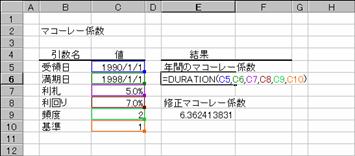 �@EX4A340Z
�@EX4A340Z
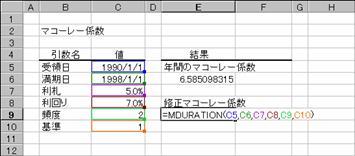 �@EX4A341Z
�@EX4A341Z
�y�܂Ƃ߁z
DURATION ����I�ɗ��q���x������،��̔N�Ԃ̃}�R�[���[�W����Ԃ��B
MDURATION �z�ʉ��i�� $100 �Ɖ��肵�āA�،��ɑ���C���}�R�[���[�W����Ԃ��B
���N���� �v ���̓c�[��
�N�����v�Z������́A���s�N�����Ɩ��ڔN���������߂��������܂��B
��EFFECT��
�w�肳�ꂽ���ڔN������ 1 �N������̕����v�Z�����ɁA�����N������Ԃ��B
��NOMINAL��
�w�肳�ꂽ�����N������ 1 �N������̕����v�Z�����ɁA���ڔN������Ԃ��B
���� EFFECT(���ڗ���, �����v�Z����)
NOMINAL(��������, �����v�Z����)
���ڗ��� ���ڔN�������w�肷��B
�������� �����N�������w�肷��B
�����v�Z���� �P�N������̕����v�Z���w�肷��B
�g�p��
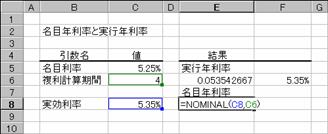
�}�`�̗�́A���ڔN������������N�����ƁA�t�̎����N�������疼�ڔN���������ꂼ��̊��ŋ��߂Ă��܂��B���̕Ԃ��l�͂P���P�O�O���Ƃ����l�Ȃ̂ŁA�\���`�����p�[�Z���g�ɐݒ肵�Č��₷�����܂��B�}�`�ł́A�Z���e�U�Ƃe�W�ɎQ�Ǝ�����͂��āA�Z���e�U�Ƃe�W�ŕ\���`�����p�[�Z���g�ɐݒ肵�Ă��܂��B
�}�`
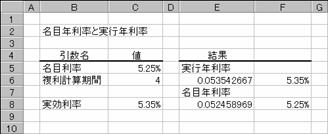 �@EX4A342Z
�@EX4A342Z
��EFFECT��
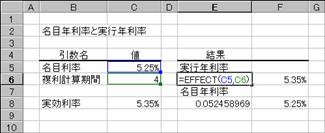 �@EX4A343Z
�@EX4A343Z
��NOMINAL��
 �@EX4A344Z
�@EX4A344Z
�y�܂Ƃ߁z
EFFECT �w�肳�ꂽ���ڔN������ 1 �N������̕����v�Z�����ɁA���s�N������Ԃ��B
NOMINAL ���ڔN������Ԃ��B
������ �v ���̓c�[��
�����ɊW������ɂ͎��̊�������܂��B
FV �����̏������l��Ԃ��B
IPMT �������ԓ��̎w�肳�ꂽ���Ɏx�����������Ԃ��B
NPER �ړI�̓����ɕK�v�Ȏx����Ԃ��B
PMT �ړI�̓����ɕK�v�Ȓ���x���z��Ԃ��B
PPMT �������ԓ��̎w�肳�ꂽ���Ɏx�����錳����Ԃ��B
PV �����̌��݉��l��Ԃ��B
RATE �����̗�����Ԃ��B
FVSCHEDULE �������ԓ��̈�A�̋������v�Z�ŏ��������̌����̏������l��Ԃ��B
���� FV(����, ����, ����x���z, ���݉��l, �x������)
���� IPMT(����, ��, ����, ���݉��l, �������l, �x������)
���� NPER(����, ����x���z, ���݉��l, �������l, �x������)
���� PMT(����, ����, ���݉��l, �������l, �x������)
���� PPMT(����, ��, ����, ���݉��l, �������l, �x������)
���� PV(����, ����, ����x���z, �������l, �x������)
���� RATE(����, ����x���z, ���݉��l, �������l, �x������, ����l)
���e�u��
��z�̎x���������I�ɍs���A���������ł���Ɖ��肵�������̏������l��Ԃ��B
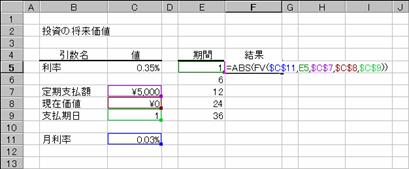
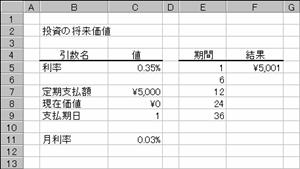
���� FV(����, ����, ����x���z, ���݉��l, �x������)
FV ���̈�������э������̏ڍׂ́APV �����Q�Ƃ��Ă��������B
���� �������Ԃ�ʂ��Ĉ��̗������w�肷��B
���� �������ԑS�̂ł̎x���̍��v���w�肷��B
����x���z ����̎x���z���w�肷��B
���݉��l ���݂̓����z�܂��͎ؓ��z�i�ȗ���0(�[��)�ƌ��Ȃ���܂��j
�x������ ����A�������A���l��0�܂���1�Ŏw�肷��B�i�ȗ���0�ƌ��Ȃ���܂��j
�x������ �x�������s���鎞��
0 �e���̊���
1 �e���̊���
�����Ɗ��Ԃ́A���ԓI�ȒP�ʂ���v������K�v������B���Ƃ��A�N���P�Q���̂S�N���[�����������ŕԍς���ꍇ�A�����͂P�Q���^�P�Q���P�i���j�A���Ԃ͂S���P�Q���S�W�i���j���w�肷��B
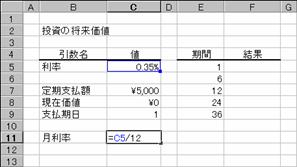
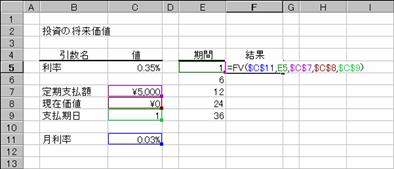
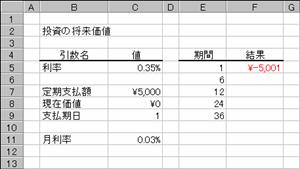
�g�p��
�m�`�n�N�����猎�����v�Z����
�m�a�n��������͂���
�m�b�n���ʂ͕����ŋ��߂���
 �@EX4A345Z
�@EX4A345Z
 �@EX4A346Z
�@EX4A346Z
 �@EX4A347Z
�@EX4A347Z
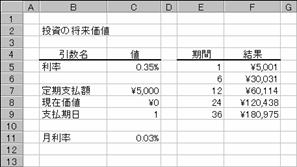
���߂�ꂽ���ʂ���₷�����邽�߂ɁA�`�a�r�����g���ĕ����i�������j���Ȃ����\���ɕύX���Ă݂܂��傤�B���͂������������̂悤�ɏ��������܂��B
�m�`�n�����������ւ���
�m�a�n���ʂ������ŋ��߂���
�m�b�n���֑����Z���ɐ����ʂ���
 �@EX4A348Z
�@EX4A348Z
 �@
�@
EX4A349Z�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A350Z
���h�o�l�s��
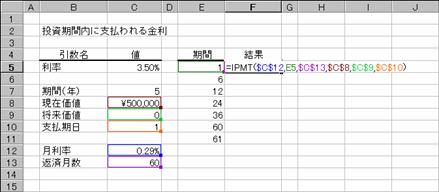
�@��z�̎x���������I�ɍs���A���������ł���Ɖ��肵�āA�������ԓ��̎w�肳�ꂽ���Ɏx�����������Ԃ��B
���� IPMT(����, ��, ����, ���݉��l, �������l, �x������)
���� �������Ԃ�ʂ��Ĉ��̗������w�肷��B
�� �����x���z�����߂���� 1 �` ���� �͈̔͂Ŏw�肷��B
���� �������ԑS�̂ł̎x���̍��v���w�肷��B
���݉��l ���݂̓����z
�������l �����̏������l�i�ȗ������0���w�肵���ƌ��Ȃ����j
�x������ �x���������s���邩���i�ȗ������0���w�肵���ƌ��Ȃ����j
�x������ �x�������s���鎞��
�@0 �e���̊���
�@1 �e���̊���
�g�p��
�T�O���~��N���R�D�T���̂T�N���[���Ŏ���ꂽ�ꍇ�A�e�x�������̋����x���z�͐}�`�̂悤�ɂȂ�܂��B�x�������������i�P�j�ɂ��Ă���̂ōŏ��̂P�����ڂ̋����͂O�ɂȂ��Ă��܂��B���������ɂ���ƁA�ŏ��̌�����ԑ����Ȃ�܂��B
�m�`�n��������͂���
�m�a�n���֑����Z���ɐ����ʂ���
 �@EX4A795Z
�@EX4A795Z
 �@EX4A351Z
�@EX4A351Z
���m�o�d�q��
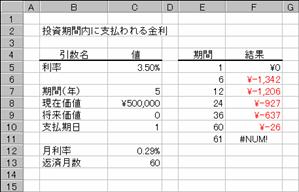
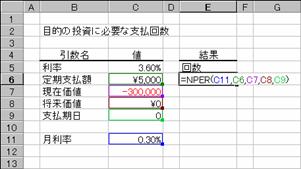
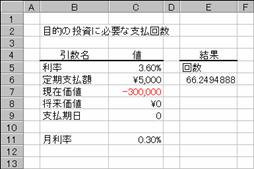
��z�̎x���������I�ɍs���A���������ł���Ɖ��肵�āA�����ɕK�v�Ȋ��Ԃ�Ԃ��B
���� NPER(����, ����x���z, ���݉��l, �������l, �x������)
���� �������Ԃ�ʂ��Ĉ��̗������w�肷��
����x���z ����̎x���z���w�肷��
���݉��l ���݂̓����z�i�ȗ������0���w�肵���ƌ��Ȃ���j
�������l �����̏������l�i�ȗ������0���w�肵���ƌ��Ȃ���j
�x������ �x���������s���邩���w�肷��B
�x������ �x�������s���鎞��
�@0 �e���̊����i�ȗ����j
�@1 �e���̊���
�g�p��
�m�`�n��������͂���
�m�a�n���ʂ����߂���
 �@
�@
EX4A353Z�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A352Z
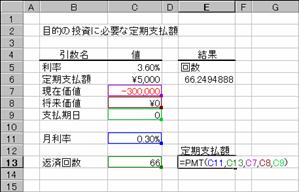
��PMT��
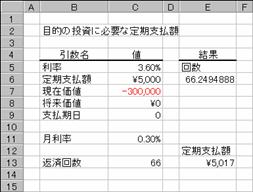
��z�̎x���������I�ɍs���A���������ł���Ɖ��肵�āA�ݕt�ɕK�v�Ȓ���x���z���Z�o���܂��B
���� PMT(����, ����, ���݉��l, �������l, �x������)
���� �ݕt���Ԃ�ʂ��Ĉ��̗������w�肷��B
���� �ݕt���ԑS�̂ł̎x���̍��v���w�肷��B
���݉��l ���݂̑ݕt�z���w�肷��
�������l �ݕt�̏������l�i�ȗ������0 (�[��)���w�肵���ƌ��Ȃ����j
�x������ �x���������s���邩���w�肷��B
�x������ �x�������s���鎞��
�@0 �e���̊����i�ȗ����j
�@1 �e���̊���
�g�p��
�m�`�n��������͂���
�m�a�n���ʂ����߂���
 �@
�@
EX4A354Z�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A355Z
���o�o�l�s��
��z�̎x���������I�ɍs���A���������ł���Ɖ��肵�āA�����̎w�肳�ꂽ���Ɏx�����錳����Ԃ��B
���� PPMT(����, ��, ����, ���݉��l, �������l, �x������)
���� �ݕt���Ԃ�ʂ��Ĉ��̗������w�肷��B
�� �����x���z�����߂����1�`���Ԃ͈̔͂Ŏw�肷��B
���� �ݕt���ԑS�̂ł̎x���̍��v���w�肷��B
���݉��l ���݂̑ݕt�z���w�肷��
�������l �ݕt�̏������l�i�ȗ������0 (�[��)���w�肵���ƌ��Ȃ����j
�x������ �x���������s���邩���w�肷��B
�x������ �x�������s���鎞��
�@0 �e���̊����i�ȗ����j
�@1 �e���̊���
�g�p��
�W�O�O���~��N���U���̂Q�O�N���[���Ŏ���ꂽ�ꍇ�A�e���i�e���j�̌����x���z�͎��̂悤�ɂȂ�܂��B
�m�`�n�N�����猎�����v�Z����
�m�a�n�N�����猎�����v�Z����
�m�b�n��������͂���
�m�c�n���ʂ͕����ŋ��߂���
�m�d�n���֑����Z���ɐ����ʂ���
 �@
�@
EX4A796Z�@�@�@�@�@�@�@�@�@�@EX4A797Z
 �@EX4A798Z
�@EX4A798Z
 �@EX4A799Z
�@EX4A799Z
��PV��
�����̌��݉��l��Ԃ��B
���� PV(����, ����, ����x���z, �������l, �x������)
���� �������Ԃ�ʂ��Ĉ��̗������w�肷��
���� �������ԑS�̂ł̎x���̍��v���w�肷��
����x���z ����̎x���z���w�肷��
�������l �����̏������l
�x������ �x���������s���邩���w�肷��B
�x������ �x�������s���鎞��
�@0 �e���̊����i�ȗ����j
�@1 �e���̊���
�g�p��
���i���T�O�O���~�̏،�������܂��B���̏،��͖����R���~�̔z�����R�O�N�Ԏx�����܂��B�N�����U���ɌŒ肳��Ă���ꍇ�̌��݉��l���v�Z���܂��B
�m�`�n���������P�ʂɂ���
�m�a�n���Ԃ����P�ʂɂ���
�m�b�n�����Ɗ��Ԃ��P�ʂɂ���
�m�c�n��������͂���
�m�d�n���ʂ����߂���
�v�Z�̌��ʁA�z�ʁi�T�O�O���j���������Ȃ��Ă���̂ō��z�����L�����Ƃ������Ƃ�������܂��B���ʂ͕����ŕ\������܂��B
 �@
�@ �@
�@
EX4A790Z�@�@�@�@�@�@�@�@�@�@EX4A791Z�@�@�@�@�@�@�@�@�@EX4A792Z
 �@
�@
EX4A793Z�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A794Z
���q�`�s�d��
�����̗�����Ԃ��B�����v�Z�̎�@���g�p����邽�߁A�����v�Z��20����s�������_�ŁA�v�Z���ʂ̎����l��0.0000001�ȉ��ɂȂ�Ȃ��ꍇ�́A�G���[�l#NUM!���Ԃ���܂��B
���� RATE(����, ����x���z, ���݉��l, �������l, �x������, ����l)
���� �������ԑS�̂ł̎x���̍��v���w�肷��B
����x���z ����̎x���z���w�肷��B
���݉��l ���݂̓����z�i�ȗ������0���w�肵���ƌ��Ȃ����j
�������l �����̏������l�i�ȗ������0���w�肵���ƌ��Ȃ����j
�x������ �x���������s���邩���w�肷��B
�x������ �x�������s���鎞��
�@0 �e���̊����i�ȗ����j
�@1 �e���̊���
����l ���������悻�ǂꂭ�炢�ɂȂ邩�𐄒肵���l���w�肷��i�ȗ���10%���w�肳���j�B
���ʂ��������Ȃ��ꍇ�́A����l�̒l��ς��Ă݂Ă��������B�ʏ�A����l�ɂO���`�P�O���͈̔͂̒l���w�肷��ƁA�v�Z���ʂ��������܂��B����l�Ɗ��Ԃ��w�肷��Ƃ��́A���ԓI�ȒP�ʂ���v������K�v������܂��B
�g�p��
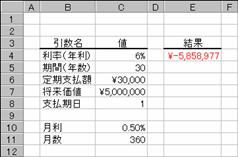
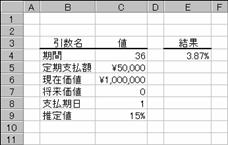
�ؓ����P�O�O���~�̃��[�����T���~���R�N�ԁi�R�U�����j�ŕԍς���ꍇ�A���[���̋����͎��̂悤�ɂȂ�܂��B���������P�ʂɂ��Ă���̂ŁA���߂��l�͌����ɂȂ�܂��B�N���́A�������P�Q�ŋ��߂邱�ƂɂȂ�܂��B
�m�`�n��������͂���
�m�a�n���ʂ����߂���i���߂�ꂽ���ʂ̕\��������K�ɐݒ肵�܂��j
 �@�@
�@�@
EX4A788Z�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A789Z
���e�u�r�b�g�d�c�t�k�d�� �v ���̓c�[��
�������ԓ��̈�A�̋������v�Z���邱�Ƃɂ��A���������̌����̏������l��Ԃ��B���̊��́A�������ϓ��܂��͒��������悤�ȓ����̏������l���v�Z����ꍇ�Ɏg�p���܂��B
���� FVSCHEDULE(����, �����z��)
���� �����̌��݉��l���w�肷��B
�����z�� �������ԓ��̕ϓ�������z��Ƃ��Ďw�肷��B
�����z��ɋZ�����w�肷��ƁA������0%�ł���ƌ��Ȃ���܂��B
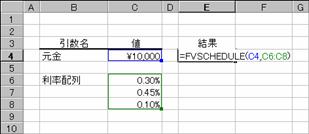
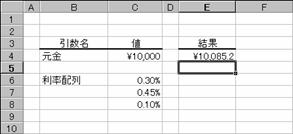
�g�p��
�����z��̃f�[�^�́A�p�[�Z���g�`���œ��͂��܂��B
�m�`�n��������͂���
�m�a�n���ʂ����߂���
 �@
�@
EX4A786Z�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A787Z
�y�܂Ƃ߁z
FV �����̏������l��Ԃ��B
IPMT �������ԓ��̎w�肳�ꂽ���Ɏx�����������Ԃ��B
NPER �ړI�̓����ɕK�v�Ȏx����Ԃ��B
PMT �ړI�̓����ɕK�v�Ȓ���x���z��Ԃ��B
PPMT �������ԓ��̎w�肳�ꂽ���Ɏx�����錳����Ԃ��B
PV �����̌��݉��l��Ԃ��B
RATE �����̗�����Ԃ��B
FVSCHEDULE �������ԓ��̈�A�̋������v�Z���邱�Ƃɂ��A���������̌����̏������l��Ԃ��B
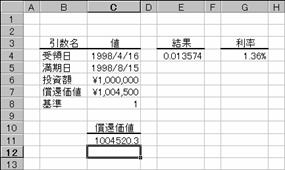
���S�z�������ꂽ�،� �v ���̓c�[��
���h�m�s�q�`�s�d��
�S�z�������ꂽ�،��̗�����Ԃ��B
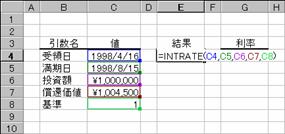
���� INTRATE(��̓�, ������, �����z, ���҉��l, �)
��̓� �،��̎�̓��i�،��̍w�����j���w�肷��
������ �،��̖������i�،��̎x�������j���w�肷��
�����z �،��ւ̓����z���w�肷��
���҉��l �������ɂ�����،��̏��Ҋz���w�肷��
� �����̌v�Z���@�𐔒l�Ŏw�肷��B�i�w��l�͂o�Q�Q�Q�Q�Ɓj�B
�g�p��
���̂悤�ȏ،�������܂��B���̏،��̗����͐}�̂悤�ɋ��߂��܂��B���ʂ͏����ŋ��߂���̂ŁA�p�[�Z���g�`���ɕύX���ĕ�����₷�����܂��B
��̓�: 1998 �N 4 �� 16 ��
������: 1998 �N 8 �� 15 ��
�����z: 1,000,000
���҉��l: 1,004,500
�: �Q�i���ۂ̓���/���ۂ̓����j
�m�`�n��������͂���
�m�a�n���ʂ����߂���
 �@
�@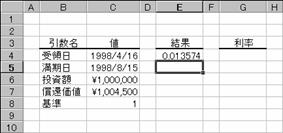
EX4A809Z�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A810Z
�m�b�n���ʂ��Q�Ƃ���Q�Ǝ�����͂���
�m�c�n�\���`�����p�[�Z���g�ɐݒ肷��
�m�d�n������K�ɒ�������
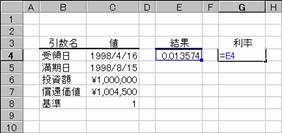 �@
�@
EX4A811Z
 �@EX4A812Z
�@EX4A812Z
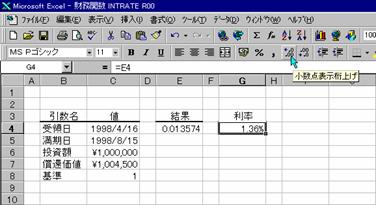 �@EX4A813Z
�@EX4A813Z
���q�d�b�d�h�u�d�c��
�S�z�������ꂽ�،��ɑ��āA�������Ɏx��������z��Ԃ��B
���� RECEIVED(��̓�, ������, �����z, ������, �)
��̓� �،��̎�̓��A�܂�،����w���������s���ȍ~�̓��t���w�肷��B
������ �،��̖������A�܂�،��̎x���������w�肷��B
�����z �،��ւ̓����z���w�肷��B
������ �،��̊��������w�肷��B
� �����̌v�Z���@�𐔒l�Ŏw�肷��B�i�w��l�͂o�Q�Q�Q�Q�Ɓj�B
�g�p��
���̂悤�ȏ����̍�������܂��B���̏،��̖������Ɏx��������z�i���҉��l�j�͎��̂悤�ɋ��߂��܂��B
��̓�: 1998 �N 4 �� 16 ��
������: 1998 �N 8 �� 15 ��
�����z: 1,000,000
������: �P�D�R�U��
�: �P�i���ۂ̓���/���ۂ̓����j
�m�`�n��������͂���
�m�a�n���ʂ����߂���
 �@
�@
EX4A814Z�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A815Z
�y�܂Ƃ߁z
INTRATE �S�z�������ꂽ�،��̗�����Ԃ��B
RECEIVED �S�z�������ꂽ�،��ɑ��āA�������Ɏx��������z��Ԃ��B
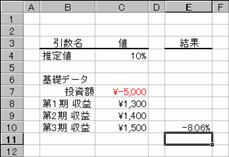
������I�ȃL���b�V���t���[
��IRR��
��A�̒���I�ȃL���b�V�� �t���[�ɑ���������v����Ԃ��B�������v���́A���̊��Ԃ��Ƃɔ�������x����(���̐�)�Ǝ��v(���̐�)����Ȃ铊��������\�������̂��Ƃł��B
���� IRR(��b�f�[�^, ����l)
��b�f�[�^ �������v�����v�Z���邽�߂̃f�[�^���w�肷��
����l �v�Z���ʂɋ߂��Ǝv���鐔�l���w�肷��
�i�ȗ���0.1(10%)���w�肳�ꂽ�ƌ��Ȃ����j
�v�Z�ɂ͔����v�Z�̎�@���g�p����܂��B����l�������l�Ƃ��A�v�Z���ʂ̌덷��0.000001%�ɂȂ�܂ŁA���v���̒l��ς��Ĕ����v�Z���s���܂��B�����v�Z��20��s���Ă��K�ȉ���������Ȃ��ꍇ�́A�G���[�l#NUM!���Ԃ���܂��B
�g�p��
���鎖�Ƃ��n�߂邽�߂ɂT�O�O�O�~�𓊎����܂����B�e���̎��v���}�̂悤�ɂȂ����ꍇ�̓������v���́A���̂悤�ɋ��߂��܂��B��b�f�[�^�Ƃ��Ďw�肷��Z���͈͂̐擪�ɂ͓����z���œ��͂��āA�e���v�z�𐳐��œ��͂��܂��B
�m�`�n��R���̓������v�������߂鐔��
�m�a�n��P���`��R���̗v�������z��������Ă���̂ŕ����̌��ʂ����߂���
 �@
�@
EX4A816Z�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A817Z
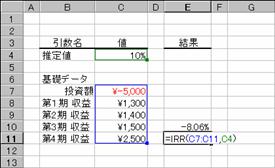
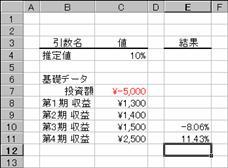
�m�b�n��S���̓������v�������߂鐔��
�m�c�n��P���`��S���̗v�������z�������Ă���̂Ő����̌��ʂ����߂���
 �@
�@
EX4A818Z�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A819Z
���l�h�q�q��
��A�̒���I�ȃL���b�V�� �t���[�Ɋ�Â��āA�C���������v����Ԃ��B���̊��ł́A���������ƌ����̍ē����ɑ����旘��(�댯����)�̗������l���ɓ�����܂��B
���� MIRR(�͈�, ���S����, �댯����)
��b�f�[�^ �������v�����v�Z���邽�߂̃f�[�^���w�肷��
���S���� �x���z(���̃L���b�V���t���[)�ɑ��闘�����w�肷��
�댯���� ���v�z(���̃L���b�V���t���[)�ɑ��闘�����w�肷��
�g�p��
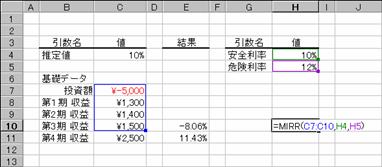
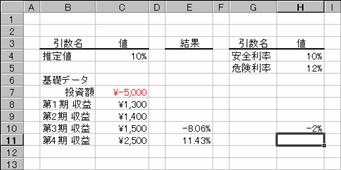
��̗�����ɁA���S�����Ɗ댯�������l���������@�œ������v�������߂�Ɛ}�̂悤�ɂȂ�܂��B�Ȃ��A�e�����ƂɎ��v��12%�̊���(�댯����)�ōē������s�����̂Ƃ��܂��B
�m�`�n��R���̓������v�������߂鐔��
�m�a�n��P���`��R���̗v�������z��������Ă���̂ŕ����̌��ʂ����߂���
 �@EX4A820Z
�@EX4A820Z
 �@EX4A821Z
�@EX4A821Z
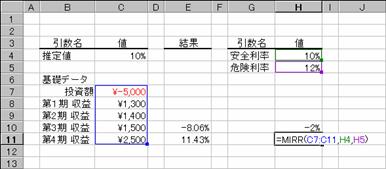
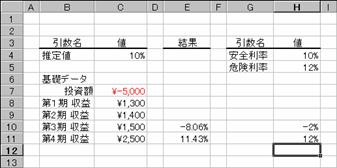
�m�b�n��S���̓������v�������߂鐔��
�m�c�n��P���`��S���̗v�������z�������Ă���̂Ő����̌��ʂ����߂���
 �@EX4A822Z
�@EX4A822Z
 �@EX4A823Z
�@EX4A823Z
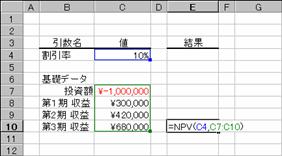
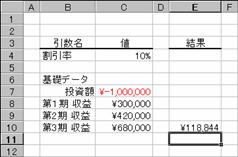
��NPV��
�����̐������݉��l���A�������A�����s�����A�̎x����(���̒l)�A����т��̎��v(���̒l)���g�p���ĎZ�o����B
���� NPV(������, �l1, �l2, ...)
������ �������Ԃ�ʂ��Ĉ��̊��������w�肷��
�l1, �l2, ... �x���z(���̒l)�Ǝ��v�z(���̒l)���w�肷��i�ő�Q�X�܂Łj
�g�p��
�P�N�ڂɂP�O�O���~�̓������s���A����ɑ����R�N�Ԃɂ��ꂼ��R�O���~�A�S�Q���~�A�U�W���~�̎��v�������߂�Ƃ��܂��B��������N���P�O���Ɖ��肵���ꍇ�A���̓����̐������݉��l�́A���̂悤�ɂȂ�܂��B
�m�`�n��R���̐������݉��l�����߂鐔��
�m�a�n���ʂ����߂���
 �@
�@
EX4A824Z�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A825Z
�y�܂Ƃ߁z
IRR ��A�̒���I�ȃL���b�V�� �t���[�ɑ���������v����Ԃ��B
MIRR ��A�̒���I�ȃL���b�V�� �t���[�Ɋ�Â��āA�C���������v����Ԃ��B
NPV ��A�̒���I�ȃL���b�V�� �t���[�Ɗ������Ɋ�Â��āA�����̐������݉��l��Ԃ��B
������I�łȂ��L���b�V���t���[
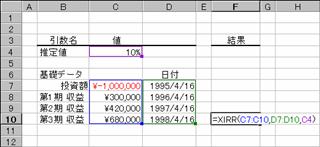
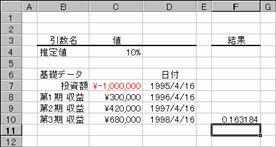
��XIRR��
����I�łȂ��L���b�V�� �t���[�ɑ���������v����Ԃ��B
���� XIRR(�͈�, ���t, ����l)
�͈� ���x���ו\�̓��t�ɑΉ������A�̃L���b�V�� �t���[���w�肷��
���t �͈͂ɑΉ������A�̎x�������w�肷��
����l �v�Z���ʂɋ߂��Ǝv���鐔�l���w�肷��
�g�p��
�}�̂悤�Ȏ��x���ו\����L���b�V���t���[�ɑ���������v�����߂Ă��܂��B���ʂ̓p�[�Z���g�l�i�P���P�O�O���Ƃ����l�j�ŋ��߂���̂ŁA�\���`�����p�[�Z���g�ɂ��āA�����ȉ��̌�����K�ɐݒ肵�܂��B
�m�`�n��R���̒l�����߂鐔��
�m�a�n���ʂ����߂���
�m�b�n�\���`�����p�[�Z���g�ɐݒ肷��
 �@
�@
EX4A826Z�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A827Z
 �@EX4A828Z
�@EX4A828Z
���w�m�o�u��
����I�łȂ��L���b�V�� �t���[�ɑ��鐳�����݉��l��Ԃ��B
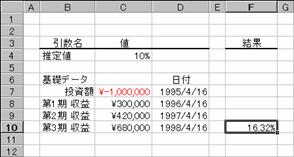
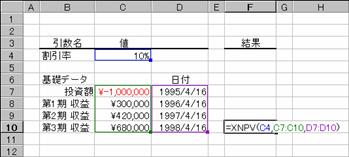
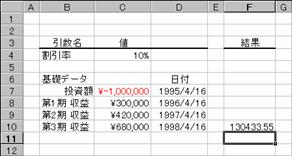
���� XNPV(������, �L���b�V���t���[, ���t)
������ �K�p���銄�������w�肷��
�L���b�V���t���[ ���x���ו\�̓��t�ɑΉ������A�̃L���b�V�� �t���[���w�肷��B
���t �L���b�V���t���[�ɑΉ������A�̎x�������w�肷��
�g�p��
�m�`�n��R���̒l�����߂鐔��
�m�a�n���ʂ����߂���
 �@EX4A829Z
�@EX4A829Z
 �@EX4A830Z
�@EX4A830Z
�y�܂Ƃ߁z
XIRR ����I�łȂ��L���b�V�� �t���[�ɑ���������v����Ԃ��B
XNPV ����I�łȂ��L���b�V�� �t���[�ɑ��鐳�����݉��l��Ԃ��B
�����������[�ȏ،�
���n�c�c�e�o�q�h�b�d��
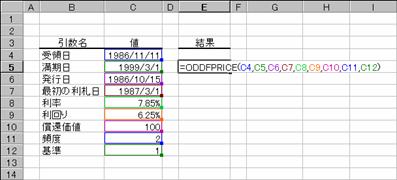
1 ���ڂ̓��������[�ȏ،��ɑ��āA�z��$100������̉��i��Ԃ��B
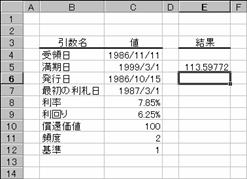
���� ODDFPRICE(��̓�, ������, ���s��, �ŏ��̗��D��, ����, �����, ���҉��l, �p�x, �)
��̓� �،��̎�̓��i�w���������t�j���w�肷��
������ �،��̖������i�،��̎x�������j���w�肷��
���s�� �،��̔��s�����w�肷��B
�ŏ��̗��D�� �،��̍ŏ��̗����x�������w�肷��B
���� �@ �،��̗������w�肷��B
����� �@ �،��̔N�Ԕz�����w�肷��B
���҉��l �z��$100�ɑ���،��̏��Ҋz���w�肷��B
�p�x �@ �N�Ԃ̗����x�����w�肷��B�P���N1��A�Q���N2��A�S���l��������
� �@ �����̌v�Z���@�𐔒l�Ŏw�肷��B�i�w��l�͂o�Q�Q�Q�Q�Ɓj�B
�������̒��ӎ����͂o�Q�Q�Q�Q��
�g�p��
���̂悤�ȏ����̍��̊z��$100������̉��i�͎��̂悤�ɋ��߂��܂��B
��̓�: 1986 �N 11 �� 11 ��
������: 1999 �N 3 �� 1 ��
���s��: 1986 �N 10 �� 15 ��
�ŏ��̗��D��: 1987 �N 3 �� 1 ��
����: 7.85%
�����: 6.25%
���҉��l: $100
�����x����: �N 2 ��
�: ���ۂ̓���/���ۂ̓���
�m�`�n��������͂���
�m�a�n���ʂ����߂���
 �@EX4A831Z
�@EX4A831Z
 �@EX4A832Z
�@EX4A832Z
���n�c�c�e�x�h�d�k�c��
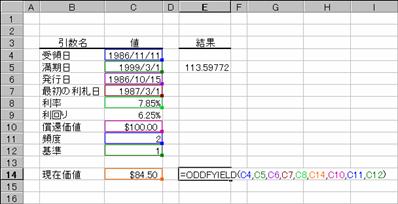
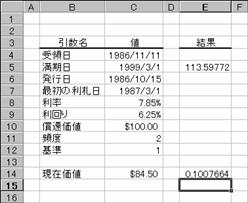
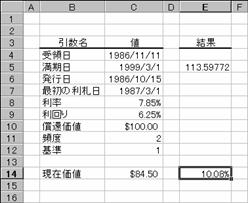
1 ���ڂ̓��������[�ȏ،��̗�����Ԃ��B
���� ODDFYIELD(��̓�, ������, ���s��, �ŏ��̗��D��, ����, ���݉��l, ���҉��l, �p�x, �)
��̓� �،��̎�̓��i�w���������t�j���w�肷��
������ �،��̖������i�،��̎x�������j���w�肷��
���s�� �،��̔��s�����w�肷��B
�ŏ��̗��D�� �،��̍ŏ��̗����x�������w�肷��B
���� �@ �،��̗������w�肷��B
���݉��l �،��̉��i���w�肷��B
���҉��l �z��$100�ɑ���،��̏��Ҋz���w�肷��B
�p�x �@ �N�Ԃ̗����x�����w�肷��B�P���N1��A�Q���N2��A�S���l��������
� �@ �����̌v�Z���@�𐔒l�Ŏw�肷��B�i�w��l�͂o�Q�Q�Q�Q�Ɓj�B
�g�p��
���̂悤�ȏ����̍��̗����������߂�Ɛ}�̂悤�ɂȂ�܂��B
��̓�: 1986 �N 11 �� 11 ��
������: 1999 �N 3 �� 1 ��
���s��: 1986 �N 10 �� 15 ��
�ŏ��̗��D��: 1987 �N 3 �� 1 ��
����: 7.85%
�����: 6.25%
���҉��l: $100
�����x����: �N 2 ��
���݉��l: $84.50
�: ���ۂ̓���/���ۂ̓���
�m�`�n��������͂���
�m�a�n���ʂ����߂���
�m�b�n�\���`�����p�[�Z���g�ɂ��Č�����K�ɐݒ肷��
 �@EX4A833Z
�@EX4A833Z
 �@�@
�@�@
EX4A834Z�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A835Z
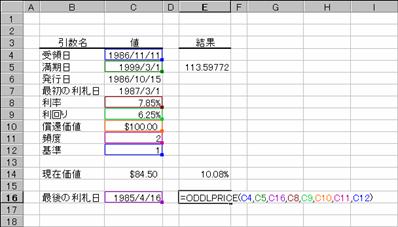
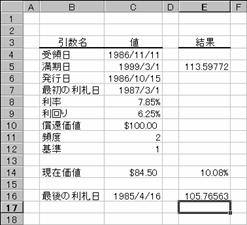
���n�c�c�k�o�q�h�b�d��
1 ���ڂ̓��������[�ȏ،��ɑ��āA�z�� $100 ������̉��i��Ԃ��B
���� ODDLPRICE(��̓�, ������, �Ō�̗��D��, ����, �����, ���҉��l, �p�x, �)
��̓� �،��̎�̓��i�w���������t�j���w�肷��
������ �،��̖������i�،��̎x�������j���w�肷��
�ŏ��̗��D�� �،��̍ŏ��̗����x�������w�肷��B
���� �@ �،��̗������w�肷��B
����� �،��̔N�Ԕz�����w�肷��B
���҉��l �z��$100�ɑ���،��̏��Ҋz���w�肷��B
�p�x �@ �N�Ԃ̗����x�����w�肷��B�P���N1��A�Q���N2��A�S���l��������
� �@ �����̌v�Z���@�𐔒l�Ŏw�肷��B�i�w��l�͂o�Q�Q�Q�Q�Ɓj�B
�g�p��
���̂悤�ȏ����̍��̊��̒l�����߂�Ɛ}�̂悤�ɂȂ�܂��B
��̓�: 1986 �N 11 �� 11 ��
������: 1999 �N 3 �� 1 ��
�Ō�̗��D��: 1985 �N�S���P�U��
����: 7.85%
�����: 6.25%
���҉��l: $100
�����x����: �N 2 ��
�: �P�i���ۂ̓���/���ۂ̓����j
�m�`�n��������͂���
�m�a�n���ʂ����߂���
 �@EX4A836Z
�@EX4A836Z
 �@EX4A837Z
�@EX4A837Z
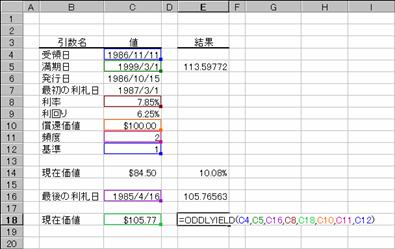
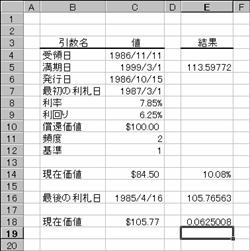
���n�c�c�k�x�h�d�k�c��
�ŏI���̓��������[�ȏ،��̗�����Ԃ��B
���� ODDLYIELD(��̓�, ������, �Ō�̗��D��, ����, ���݉��i, ���҉��l, �p�x, �)
��̓� �،��̎�̓��i�w���������t�j���w�肷��
������ �،��̖������i�،��̎x�������j���w�肷��
�ŏ��̗��D�� �،��̍ŏ��̗����x�������w�肷��B
���� �@ �،��̗������w�肷��B
���݉��l �،��̉��i���w�肷��B
���҉��l �z��$100�ɑ���،��̏��Ҋz���w�肷��B
�p�x �@ �N�Ԃ̗����x�����w�肷��B�P���N1��A�Q���N2��A�S���l��������
� �@ �����̌v�Z���@�𐔒l�Ŏw�肷��B�i�w��l�͂o�Q�Q�Q�Q�Ɓj�B
�g�p��
���̂悤�ȏ����̍��̊��̒l�����߂�Ɛ}�̂悤�ɂȂ�܂��B
��̓�: 1986 �N 11 �� 11 ��
������: 1999 �N 3 �� 1 ��
�Ō�̗��D��: 1985 �N�S���P�U��
����: 7.85%
���݉��l: $�P�O�T�D�V�V
���҉��l: $100
�����x����: �N 2 ��
�: �P�i���ۂ̓���/���ۂ̓����j
�m�`�n��������͂���
�m�a�n���ʂ����߂���
�m�b�n�\���`�����p�[�Z���g�ɂ��Č�����K�ɐݒ肷��
 �@EX4A838Z
�@EX4A838Z
 �@�@
�@�@
EX4A839Z�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A840Z
�y�܂Ƃ߁z
ODDFPRICE 1 ���ڂ̓��������[�ȏ،��ɑ��āA�z�� $100 ������̉��i��Ԃ��B
ODDFYIELD 1 ���ڂ̓��������[�ȏ،��̗�����Ԃ��B
ODDLPRICE 1 ���ڂ̓��������[�ȏ،��ɑ��āA�z�� $100 ������̉��i��Ԃ��B
ODDLYIELD �ŏI���̓��������[�ȏ،��̗�����Ԃ��B
������I�ɗ������x������،� �v ���̓c�[��
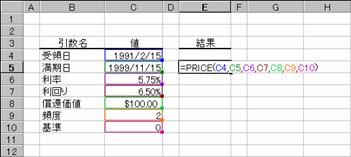
��PRICE��
����I�ɗ������x������،��ɑ��āA�z��$100������̉��i��Ԃ��B
���� PRICE(��̓�, ������, ����, �����, ���҉��l, �p�x, �)
��̓� �،��̎�̓��i�،����w���������t�j���w�肷��B
������ �،��̖������i�،��̎x�������j���w�肷��B
���� �،��̔N�����w�肷��B
����� �،��̔N�Ԕz�����w�肷��B
���҉��l �z��$100�ɑ���،��̏��Ҋz���w�肷��B
�p�x �N�Ԃ̗����x�����w�肷��B�P���N1��A�Q���N2��A�S���l��������
� �����̌v�Z���@�𐔒l�Ŏw�肷��B�i�w��l�͂o�Q�Q�Q�Q�Ɓj�B
�g�p��
���̂悤�ȏ����̍��̏ꍇ�A�z��$100������̉��i�͐}�̂悤�ɋ��߂��܂��B
��̓�: 1991 �N 2 �� 15 ��
������: 1999 �N 11 �� 15 ��
����: 5.75%
�����: 6.50%
���҉��l: $100
�����x����: �N 2 ��
�: �O�i36 ��/360 ���j
�m�`�n��������͂���
�m�a�n���ʂ����߂���
 �@
�@
EX4A841Z�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A842Z
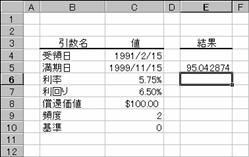
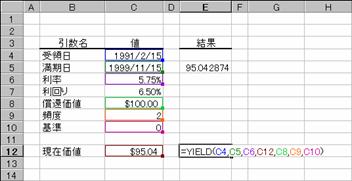
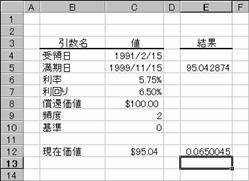
��YIELD��
����������I�Ɏx������،��̗�����Ԃ��B���̊��́A���̗������v�Z����Ƃ��Ɏg�p���܂��B
YIELD(��̓�, ������, ����, ���݉��l, ���҉��l, �p�x, �)
��̓� �،��̎�̓��i�،����w���������t�j���w�肷��B
������ �،��̖������i�،��̎x�������j���w�肷��B
���� �،��̔N�����w�肷��B
���݉��l �z��$100�ɑ���،��̉��i���w�肷��B
���҉��l �z��$100�ɑ���،��̏��Ҋz���w�肷��B
�p�x �N�Ԃ̗����x�����w�肷��B�P���N1��A�Q���N2��A�S���l��������
� �����̌v�Z���@�𐔒l�Ŏw�肷��B�i�w��l�͂o�Q�Q�Q�Q�Ɓj�B
�g�p��
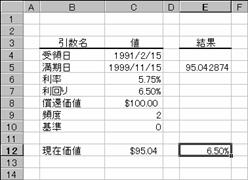
���̂悤�ȏ����̍��̏ꍇ�A�،��̗����͐}�̂悤�ɋ��߂��܂��B
��̓�: 1991 �N 2 �� 15 ��
������: 1999 �N 11 �� 15 ��
����: 5.75%
���݉��l: $95.04287
���҉��l: $100
�����x����: �N 2 ��
�: �O�i30��/360���j
�m�`�n��������͂���
�m�a�n���ʂ����߂���
�m�b�n�\���`�����p�[�Z���g�ɂ��Č�����K�ɐݒ肷��
 �@EX4A843Z
�@EX4A843Z
 �@�@
�@�@
EX4A844Z�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A845Z
�y�܂Ƃ߁z
PRICE ����I�ɗ������x������،��ɑ��āA�z�� $100 ������̉��i��Ԃ��B
YIELD ����������I�Ɏx������،��̗�����Ԃ��B
���������ɗ������x������،� �v ���̓c�[��
���o�q�h�b�d�l�`�s��
�������ɗ������x������،��ɑ��Ċz��$100������̉��i��Ԃ��B
���� PRICEMAT(��̓�, ������, ���s��, ����, �����, �)
��̓� �،��̎�̓��A�܂�،����w���������s���ȍ~�̓��t���w�肷��B
������ �،��̖������A�܂�،��̎x���������w�肷��B
���s�� �،��̔��s�����w�肷��B
���� ���s���ɂ�����،��̗������w�肷��B
����� �،��̔N�Ԕz�����w�肷��B
���݉��l �z�� $100 �ɑ���،��̉��i���w�肷��B
� �����̌v�Z���@�𐔒l�Ŏw�肷��i�w��l�͂o�Q�Q�Q�Q�Ɓj
�������̒��ӎ����͂o�Q�Q�Q�Q��
�g�p��
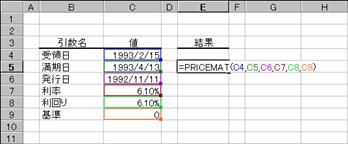
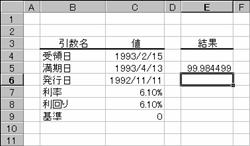
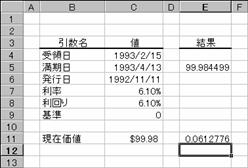
���̂悤�ȏ����̍��̏ꍇ�A�z��$100������̉��i�͐}�̂悤�ɋ��߂��܂��B
��̓�: 1993 �N 2 �� 15 ��
������: 1993 �N 4 �� 13 ��
���s��: 1992 �N 11 �� 11 ��
����: 6.1%
�����: 6.1%
�:�O�i30��/360���j
�m�`�n��������͂���
�m�a�n���ʂ����߂���
 �@
�@
EX4A846Z�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A847Z
���x�h�d�k�c�l�`�s�� �v ���̓c�[��
�������ɗ������x������،��̗�����Ԃ��B
���� YIELDMAT(��̓�, ������, ���s��, ����, ���݉��l, �)
��̓� �،��̎�̓��A�܂�،����w���������s���ȍ~�̓��t���w�肷��B
������ �،��̖������A�܂�،��̎x���������w�肷��B
���s�� �،��̔��s�����A���t�̃V���A���l�Ŏw�肷��B
���� ���s���ɂ�����،��̗������w�肷��B
� �����̌v�Z���@�𐔒l�Ŏw�肷��B�i�w��l�͂o�Q�Q�Q�Q�Ɓj�B
�g�p��
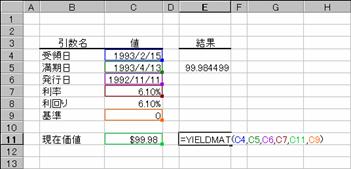
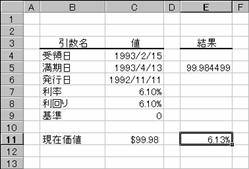
���̂悤�ȏ����̍��̏ꍇ�A�،��̗����͐}�̂悤�ɋ��߂��܂��B
��̓�: 1993 �N 2 �� 15 ��
������: 1993 �N 4 �� 13 ��
���s��: 1992 �N 11 �� 11 ��
����: 6.1%
���݉��l: $�X�X�D�X�W
�:�O�i30��/360���j
�m�`�n��������͂���
�m�a�n���ʂ����߂���
�m�b�n�\���`�����p�[�Z���g�ɂ��Č�����K�ɐݒ肷��
 �@EX4A848Z
�@EX4A848Z
 �@
�@
EX4A849Z�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A850Z
�y�܂Ƃ߁z
PRICEMAT �������ɗ������x������،��ɑ��āA�z�� $100 ������̉��i��Ԃ��B
YIELDMAT �������ɗ������x������،��̗�����Ԃ��B
���č������ȒZ���،� �v ���̓c�[��
�č������ȒZ���،��ɊW����R�̊�������܂��BTBILLEQ���͕č������ȒZ���،�(TB)�̍��ɑ������闘���ATBILLPRICE���͕č������ȒZ���،�(TB)�̊z��$100������̉��i�ATBILLYIELD���͕č������ȒZ���،�(TB)�̗�����Ԃ��B
���� TBILLEQ(��̓�, ������, ������)
���� TBILLPRICE(��̓�, ������, ������)
���� TBILLYIELD(��̓�, ������, ���݉��l)
��̓� �����ȏ،��̎�̓��i�w���������t�j���w�肷��
������ �����ȏ،��̖������i�x�������j���w�肷��
������ �����ȏ،��̊��������w�肷��
���݉��l �z��$100�ɑ�������ȏ،��̉��i���w�肷��
�������̒��ӎ����͂o�Q�Q�Q�Q��
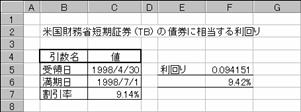
���s�a�h�k�k�d�p���̗�
 �@EX4A141Z
�@EX4A141Z
F5: =TBILLEQ(C5,C6,C7)
F6: =F5
���߂��l�̓p�[�Z���g�l�ɂȂ�̂ŁA�\���`�������ɐݒ肵�Č��ʂ���₷�����܂��B�Z���e�T�����ɐݒ肵�Ă������̂ł����A�����ł͕\���`���ɂ��l�̌ܓ��̌��ʂƌ���ׂ邽�߂ɁA�Q�Ǝ��Œl���Z���e�U�Ɏʂ��ăp�[�Z���g��ݒ肵�Ă��܂��B�����_�ȉ��̌����͓K�ɐݒ肵�܂��B�Ȃ��A�����ɓ��t�ړ��͂���ꍇ�́Amm/dd/yy�`���Łh�h�ň͂�œ��͂��܂��B
TBILLEQ("4/30/98","7/1/98",0.0914)
�Q�l
TBILLEQ ���́A���̐����ŕ\����܂��B
TBILLEQ = (365 x ����) / (360 - (���� x DSM))
������
DSM = ��̓����疞�����܂ł̓��� (�����v�Z�̊�ƂȂ�1�N�̓�����360��)
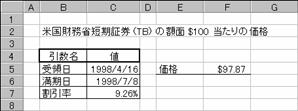
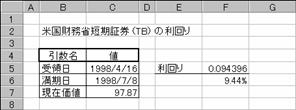
���s�a�h�k�k�o�q�h�b�d���̗�
 �@EX4A142Z
�@EX4A142Z
F5: =TBILLPRICE(C5,C6,C7)
���s�a�h�k�k�x�h�d�k�c���̗�
 �@EX4A143Z
�@EX4A143Z
F5: =TBILLYIELD(C5,C6,C7)
F6: =F5
�y�܂Ƃ߁z
TBILLEQ �č������ȒZ���،�(TB)�̍��ɑ������闘����Ԃ��B
TBILLPRICE �č������ȒZ���،�(TB)�̊z��$100������̉��i��Ԃ��B
TBILLYIELD �č������ȒZ���،�(TB)�̗�����Ԃ��B
���h�����i�̏���/�����\��
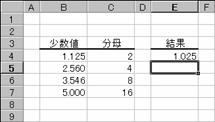
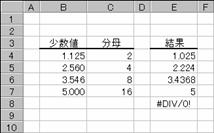
���c�n�k�k�`�q�e�q�� �v ���̓c�[��
�����ŕ\���ꂽ�h�����i���\���ɕϊ�����B
���� DOLLARFR(�����l, ����)
�����l �����ŕ\���ꂽ���l���w�肷��B
���� �����̕���ƂȂ鐮�����w�肷��B
����ɐ����ȊO�̒l���w�肷��Ə����_�ȉ�����̂Ă��܂��B���ꂪ�O�ł���ꍇ�A�G���[�l#�c�h�u�^�O�I���Ԃ���܂��B
�g�p��
�m�`�n��������͂���
�m�a�n���ʂ����߂���
�m�b�n���֑����Z���ɐ����ʂ���
�Z���d�W�̏ꍇ�́A�l�����͂���Ă��Ȃ��̂ŁA���ꂪ�O�ƂȂ�G���[���\������Ă��܂��B�l�O����͂��Ă������G���[���\���i�Ԃ���j����܂��B
 �@
�@
EX4A803Z�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A804Z
 �@EX4A805Z
�@EX4A805Z
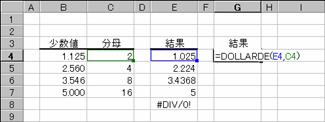
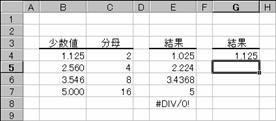
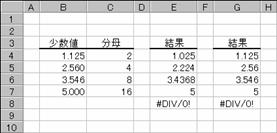
���c�n�k�k�`�q�c�d�� �v ���̓c�[��
�����ŕ\���ꂽ�h�����i���A�����\���ɕϊ����܂��B
���� DOLLARDE(���q, ����)
���q �����ŕ\���ꂽ���l���w�肷��B
���� �����̕���ƂȂ鐮�����w�肷��B
����ɐ����ȊO�̒l���w�肷��Ə����_�ȉ�����̂Ă��܂��B���� 0�ł���ꍇ�A�G���[�l #NUM! ���Ԃ���܂��B
�g�p��
�m�`�n��������͂���
�m�a�n���ʂ����߂���
�m�b�n���֑����Z���ɐ����ʂ���
 �@
�@
EX4A806Z�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A807Z
 �@EX4A808Z
�@EX4A808Z
�y�܂Ƃ߁z
DOLLARDE �����ŕ\���ꂽ�h�����i���A�����\���ɕϊ����܂��B
DOLLARFR �����ŕ\���ꂽ�h�����i���A�����\���ɕϊ����܂��B
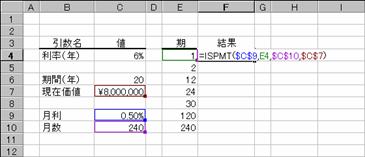
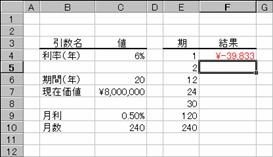
��ISPMT��
�������ԓ��̎w�肳�ꂽ���Ɏx�����������Ԃ��B���̊��́ALotus1-2-3���Ƃ̌݊�����ۂ��߂ɗp�ӂ���Ă��܂��B
���� ISPMT(����, ��, ����, ���݉��l)
���� �������Ԃ�ʂ��Ĉ��̗������w�肷��B
�� �����x���z�����߂����1�`���Ԃ͈̔͂Ŏw�肷��B
���� �������ԑS�̂ł̎x���̍��v���w�肷��B
���݉��l ���݂̓����z�w�肷��
�������̒��ӎ����͂o�Q�Q�Q�Q��
�g�p��
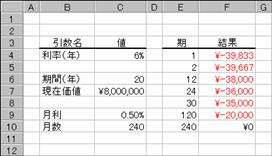
�ؓ����W�O�O���~��N���U���̂Q�O�N���[���Ŏ���ꂽ�ꍇ�A�e���i�e���j�̋����x���z�͎��̂悤�ɋ��߂��܂��B�i�����A�����͂o�Q�Q�Q���Q�l�j
�m�`�n��������͂���
�m�a�n���ʂ����߂���
�m�b�n���֑����Z���ɐ����ʂ���
 �@EX4A800Z
�@EX4A800Z
 �@
�@
EX4A801Z�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@EX4A802Z
�y�܂Ƃ߁z
ISPMT �������ԓ��̎w�肳�ꂽ���Ɏx�����������Ԃ�
�쐬�菇
�@���āA�ǂ����珑���n�߂�����̂ł��傤�B

 |